Filtern ist für mehrere Zwecke im Prozess der Oberflächenbeschaffenheitsanalyse erforderlich. Ein morphologisches Filter wird gewöhnlich verwendet, um den Effekt der Tastspitze auf Rohdaten zu korrigieren; ein Filter zum Entfernen von Ausreißern kann benötigt werden, um Daten zu filtern, die mit einem optischen Sensor aufgenommen wurden. In einigen Fällen ist ein Glättfilter erforderlich, wie zum Beispiel ein λs or S-Filter, um Daten zu vergleichen, die mit verschiedenen Methoden gemessen wurden. Aber der Hauptgrund für die Verwendung eines Filters ist die Trennung von langskaligen Komponenten und kurzskaligen Komponenten, d.h. von Welligkeit und Rauheit, und die Parameter gemäß der Spezifikation zu berechnen.
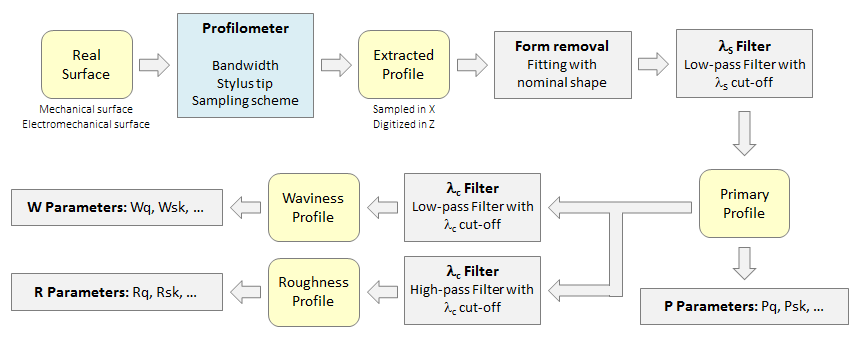
[ISO 3274] definiert ein Messschema wie oben. Ein von einem modernen Profilometer gemessenes Profil wird Profilschnitt genannt. Es ist gesampelt und digitalisiert, und stellt eine Abstraktion der wirklichen Oberfläche dar (mehrere Filtereffekte werden durch den Taster und die Bandbreite des Instruments eingeführt). Die wirkliche Oberfläche kann durch eine mechanische Oberfläche (Grenze) modelliert werden, wenn sie mit einem Taster gemessen wird, oder durch eine elektromagnetische Oberfläche, die die Oberflächengrenze darstellt , die von einem optischen Sensor gemessen wurde. Der nächste Schritt besteht darin, Form zu entfernen, entweder durch Angleichung der nominalen Form des Bauteils (z. B. eines Kreises), oder durch Angleichung eines Polynoms, um das Profil auszurichten oder zu verflachen. Der nächste Schritt ist dann das λs-Filtern, um die Mikrorauheit zu entfernen, die meistens durch Instrument- oder Umgebungs-Rauschen verursacht wird. Manchmal wird dieser Schritt übersprungen, zum Beispiel in der deutschen Norm [VDA 2006] aus der Automobilindustrie. Das somit erhaltene Profil wird Primärprofil genannt. Einige P-Parameter können auf diesem Profil berechnet werden. Dann wird das λc-Filter angewandt, das Welligkeit von Rauheit trennt. Dann können Rauheits- oder Welligkeits-Parameter berechnet werden.
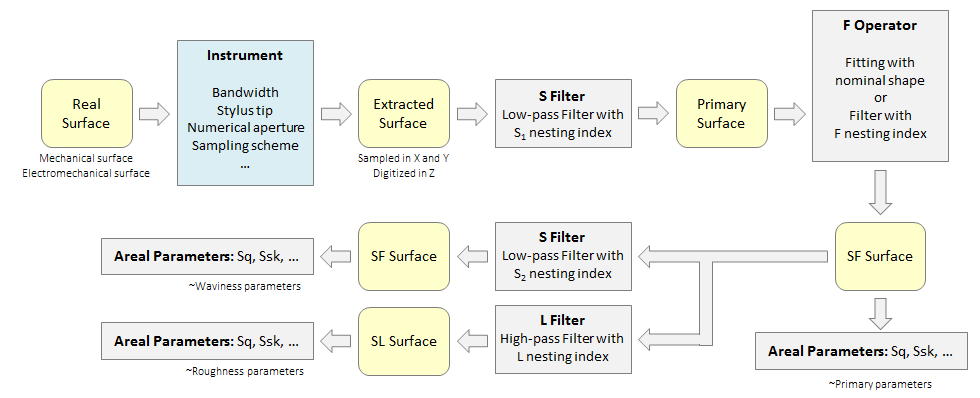
Ein ähnliches Schema (oben) kann für (flächenhafte) Oberflächen erstellt werden. Das in ISO 25178 eingeführte Vokabular ist neu aber eher leicht verständlich: Das S-Filter entfernt kurz-skalige Komponenten. Das L-Filter entfernt lang-skalige Komponenten. Der F-Operator entspricht der Form-Entfernung. Skalenbegrenzte Oberflächen - eine SF-Oberfläche oder eine SL-Oberfläche - werden durch Anwendung der jeweiligen Filter/Operationen erhalten. Flächenhafte Parameter enthalten in ihrem Namen keinen Hinweis auf die vorhergehende Filter-Operation.
Historische Filter
Die ersten Filter wurden als physikalische Hochpassfilter implementiert, wobei Widerstände und Kondensatoren hinter einen Selektor gelötet wurden. Das anfängliche Ziel bestand darin, große Signalschwankungen zu vermeiden, um das Profil korrekt auf einem Thermopapierband zu zeichnen, oder um eine Rauheitsdurchschnittsanzeige auf einer Anzeigenskala anzuzeigen. Diese RC-Filter wurden fast 30 Jahren auf allen Arten von Tast-Profilometern verwendet. In den 1980er Jahren fing man an, Personalcomputer als Analysegeräte verwendet, die über Analog/Digital-Platinen mit Profilometern verbunden waren. Die ersten Profilanalyseprogramme implementierten das RC-Filter mit einem Algorithmus, um die gleiche Menge wie das analoge Filter zu filtern.
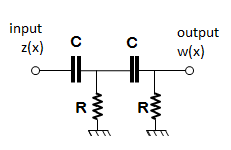

Analoger RC2-Filter (links) und Talysurf 10 mit Cut-Off-Auswahl (rechts)
Der Hauptnachteil dieses Filters ist die Phasenverzerrung seiner Transferfunktion. Jede Wellenlänge im ursprünglichen Profil wird unterschiedlich verschoben, was zu kritischen Problemen um Stufen, Rillen und Spitzen herum führt.
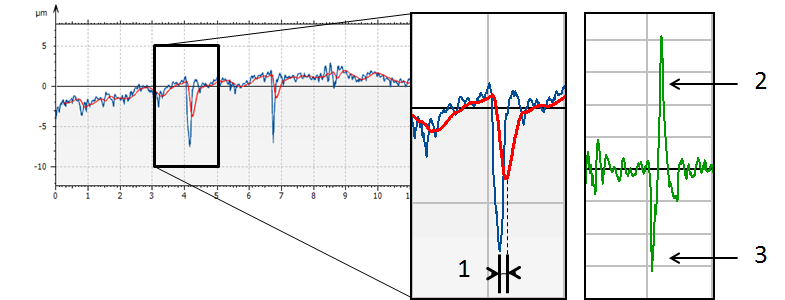
Analoger RC2-Filter
Oberhalb: Zoom auf die Phasenverschiebung (1) in einer Furche. Die Mittelwertlinie hängt dem Primärprofil hinterher. Das führt auf dem Rauheitsprofil (an der Stelle, wo die Furche ist) zu überhöhten Spitzen (2) und zu einer verkleinerten Furchentiefe (3).
Zu Beginn der 1990er Jahre wurde eine phasenkorrekte Version des RC2-Filters erstellt, um dieses Problem zu beheben. Diese Version wurde RC2-PC genannt. Allerdings war eine noch tiefgründigere Arbeit im Gange, um ein nativ phasenkorrektes Filter zu erzeugen, das Gauß-Filter.
Gauß-Filter
Das Gauß-Filter für Profile wurde 1996 in der Norm ISO 11562 eingeführt. Die Norm definiert eine Transferfunktion für das Low-Pass-Filter, das das Welligkeits-Profil erzeugt (Mittelwertlinie). Die Subtraktion dieser Mittelwertlinie vom Primärprofil ergibt das Rauheitsprofil.
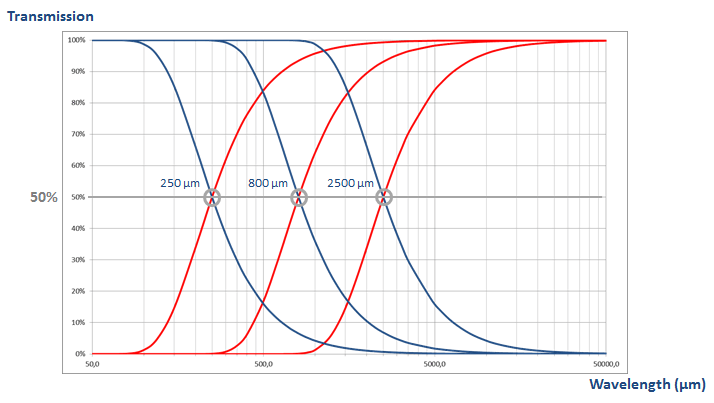
Übertragungsmerkmale für das Rauheitsfilter (blau) und das Welligkeitsfilter (rot), für mehrere Cut-off-Werte. Diese Kurven kreuzen sich bei 50 % der Übertragung.
Es ist eine gängige Praxis, jedes Ende des gefilterten Profils je nach Hersteller um eine Länge zu kürzen. Einige schneiden einen halben Cut-off an jedem Ende ab, andere schneiden einen ganzen Cut-off ab. In Theorie sollte der Wert mindestens 0,6 Cut-off betragen. Die Folge ist, dass das Rauheits- oder Welligkeitsprofil 1 oder 2 Cut-off kürzer als das Primärprofil ist.
In MountainsMapkönnen Benutzer die Länge auswählen, die vom gefilterten Profil abgeschnitten wird, und verfügen über eine Option zum Verwalten von End-Effekten, um die volle Länge zu behalten.
2011 wurde [ISO 16610-21] die offizielle Norm, die das Gauß-Filter für offene oder geschlossene Profile definiert hat, und ersetzt die ältere Norm ISO 11562. Die entsprechende Definition für Oberflächen finden Sie in [ISO 16610-61].
Weitere Details zu Flächenfiltern finden Sie in [SEEWIG 2013]
Am Cut-Off-Wert überträgt der Filter 50 % der Amplitude der Wellenlänge. Filter sollten nicht als Tore gesehen werden, die Wellenlängen plötzlich blockieren; Die Übertragungseigenschaften sind kontinuierlich und progressiv. Daher ist die Wahl des Cut-off-Wertes je nach Anwendung ein sehr wichtiger Punkt, um diejenigen Wellenlängen (oder Skalen) korrekt zu trennen, die zu den jeweilig interessanten Komponenten der Oberflächenbeschaffenheit gehören.
Gauß-Filter werden seit 20 Jahren erfolgreich für verschiedene Anwendungen in Industrie und Forschung eingesetzt. Allerdings verhält sich dieses Filter in der Umgebung von Ausreißern und Stufen und in Gegenwart von Form nicht besonders gut. Das ist der Grund, warum robuste Filter entwickelt worden sind.
Robuste Gauß-Filter
Bei einem robusten Filter folgt die Mittelwertlinie (Mittelwertebene) korrekt dem allgemeinen Trend des Profils (der Oberfläche), ohne von Ausreißern gestört zu werden. Das Robuste Regressions-Gauß-Filter ist in [ISO 16610-31] als iterativer Algorithmus definiert, das lokale Gewichte je nach Abstand zwischen Primärprofil und Welligkeitsprofil berechnet.

Das Gaußsche Filter (links) wird durch lokale Diskontinuitäten gestört, bei dem Robusten Gauß-Filter (rechts) ist das nicht der Fall.
Das Robuste Gauß-Filter ist die bevorzugte Wahl für strukturierte und vielschichtige (plateauartige) Oberflächen, und für Form, Rillen oder Poren. Es ist insbesondere ein guter Ersatz und eine gute Verbesserung für das doppelte Gauß-Filter, das in [ISO 13565-1] (früher DIN 4777) definiert ist
Cut-off und Nesting-Index
Der Begriff Cut-off wird heute für die Wellenlänge verwendet, bei der das Filter die Wellenlänge um 50 % abschwächt. Das bedeutet ebenfalls, dass diese Wellenlänge zu 50 % übertragen wird. Benutzer sollten den Cut-off-Wert sorgfältig auswählen, wenn Wellenlängen in zwei Datensatz-Gruppen eingeteilt werden sollen, ohne zum Beispiel Werte einer Gruppe in der Mitte zu schneiden. Anders gesagt, wenn ein Werkstück Rauheit und Welligkeit enthält, dann zeigt das Spektrum einen Wellenlängen-Datensatz für Rauheit und einen anderen für Welligkeit. Der Cut-off-Wert sollte so ausgewählt werden, dass er die zwei Datensätze unterteilt, ohne sie zu verzerren. In einigen Fällen ist das Werkstück flach genug und enthält keine Welligkeit; in einem solchen Fall wird das Filter nicht benötigt.
Bei Profilen sollten Cut-off-Werte aus einer in [ISO 4288] beschriebenen Liste ausgewählt werden: ... 0,08 mm; 0,25 mm; 0,8 mm; 2,5 mm ...
Jedoch können Benutzer, die Werkstücke analysieren, die außerhalb des Geltungsbereichs des GPS-Systems liegen (welches in erster Linie mechanische Komponenten betrifft), andere Cut-off-Werte wählen. In so einem Fall sollte der Benutzer zuerst einen funktionellen Korrelations-Test durchführen, um die Entsprechung zwischen Filtertyp und Cut-off-Wert einerseits und der Leistung der überwachten Funktion andererseits zu erstellen. Stahlbleche können zum Beispiel mit einem Cut-off von 5 mm gefiltert werden, um Welligkeit zu isolieren, die von Vibrationswalzen auf das Blech übertragen wurde.
Empfehlungen für Cut-off-Werte für Oberflächen finden Sie in ISO 25178-3]: ... 0,1 mm; 0,2 mm; 0,25 mm; 0,5 mm; 0,8 mm; 1,0 mm ...
Der Begriff Nesting-Index wurde eingeführt, um das Konzept des (auf lineare Filter begrenzten) Cut-offs auf andere Filter zu erweitern. In der Normenreihe ISO 16610 werden neue nicht-lineare Filter wie das Morphologische Filter und das Robuste Spline-Filter definiert. Da der Begriff Cut-off für diese Filter nicht verwendet werden kann, wird stattdessen der Begriff Nesting-Index verwendet. Ein Nesting-Index ist ein Parameterwert, der das Filter kontrolliert, sowie die Art und Weise, wie Skalen oder Wellenlängen getrennt werden.
Im Falle des Spline-Filters ist der Nesting-Index nur der Cut-off. Bei einem morphologischem Filter entspricht der Nesting-Index der Form des strukturierenden Elementes (z. B. Kugel) und seiner Größe (Durchmesser).
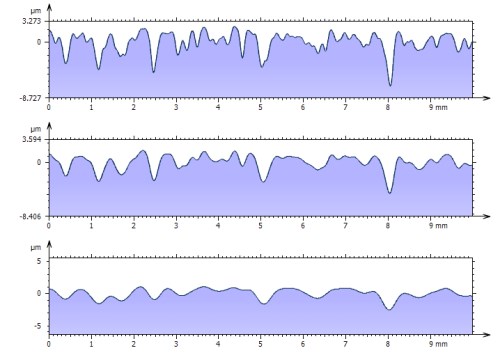
Gefilterte Profile (Welligkeit) mit verschiedenen Cut-offs
(von oben nach unten: 0,2 mm, 0,4 mm und 0,8 mm)
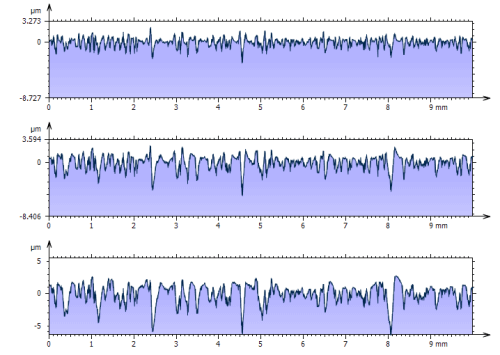
Gefilterte Profile (Rauheit) mit gleichen Cut-offs wie oben.
Kubische Spline-Filter
Kubische Splines sind geometrische Kurven, die eine Reihe von Punkten mit weichen Kurven verbinden. Splines werden zum Zeichnen von Kurvenformen in CAD-Programmen und zum Interpolieren von Datenpunkten verwendet.
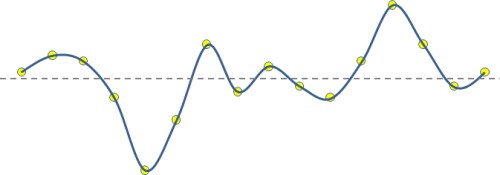
Datenpunkte (gelb), verbunden mit einer Spline-Kurve (blau).
Nach der Anwendung eines kubischen Spline-Filters geht die Spline-Kurve nicht durch die Datenpunkte, sonder durch aufgehängte Punkte. Diese Punkte sind mit den Datenpunkten über eine fiktive Feder einer gewissen Federkonstante (Härte) ß verbunden, die Spannungs-Parameter genannt wird. Das Verhalten des Filters kann kontrolliert werden, indem die Federkonstante (auf einen Wert zwischen 0 und 1) eingestellt wird.

Aufgehängte Punkte (grün), über eine elastische Feder mit den ursprünglichen Datenpunkten verbunden. Die Spline-Kurve (blau) stellt jetzt das gefilterte Profil (Welligkeit) dar.
Standardmäßig (mit β = 0.6252) ist das Verhalten des kubischen Spline-Filters dem des Gauß-Filters sehr ähnlich.
Das Kubische Spline-Filter ist in [ISO 16610-22] für Profile und in [ISO 16610-62] für Oberflächen beschrieben.
In der Praxis hat das Spline-Filter keine signifikanten Vorteile gegenüber dem Gauß-Filter.
Robuste Spline-Filter
Eine Variante wurde entworfen, um der Definition des Spline-Filters Robustheit zu verleihen. Der Robuste Spline-Filter ist in [ISO 16610-32] für Profile und [ISO 16610-62] für Oberflächen definiert. Aufgrund seiner nicht-linearen Natur ist seine Implementierung recht komplex; deswegen wird dieses Filter nur sehr selten in Analyse-Software verwendet.
Obwohl dieses robuste Filter theoretisch besser als das Robuste Gauß-Filter ist, sind die Ergebnisse in beiden Fällen sehr ähnlich; da das Robuste Gauß-Filter viel einfacher zu implementieren ist, wird es in den meisten Fällen bevorzugt.
Wavelet-Filter
Wavelet-Filter basieren auf lokalisierter harmonischer Analyse mit kurzfristigen Signalen, die Mutter-Wavelets genannt werden. Bei der Analyse von Oberflächenbeschaffenheit werden Wavelet-Filter verwendet, um Profile und Oberflächen in verschiedene Skalen zu unterteilen. Somit können einzelne Skalen identifiziert werden, in denen ein besonderes Phänomen auftritt; ebenfalls können Merkmale auf einer bestimmten Skala entfernt werden, und das Signal ohne dieses Merkmal (Ausreißer oder Struktur) wieder rekonstruiert werden.
Wavelet-Filter sind in [ISO 16610-29] für Profile und [ISO 16610-69] für Oberflächen beschrieben. Aktuell beschreibt die Norm nur Spline-Wavelets. Komplexe Wavelets sollten in Zukunft hinzugefügt werden, vor allem für Oberflächen. In der Literatur werden viele andere Arten von Wavelets (Coiflet, Daubechies, ...) beschrieben, die für spezifische Anwendungen wie Infrarot-Bildanalyse oder Erdbebensignalen verwendet werden, die aber bei der Analyse von Oberflächenstruktur weniger interessant sind.
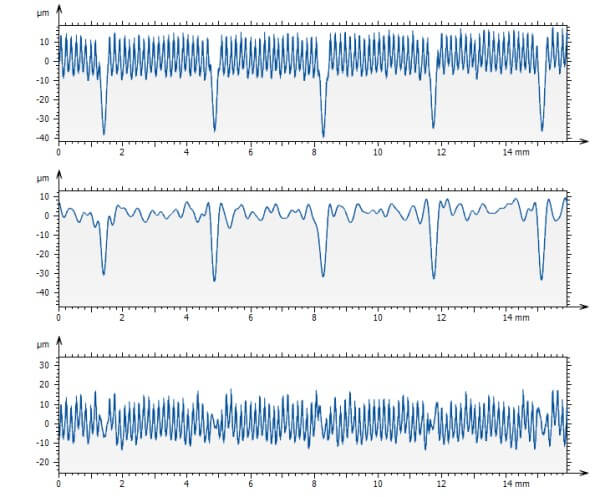
Oben: ein Profil, das zwei überlagerte periodische Strukturen enthält, und mit einem Diskreten Wavelet-Filter unter Verwendung einer Meyer-Wavelet gefiltert wird. Die beiden Signale sind für weitere Analyse klar getrennt.
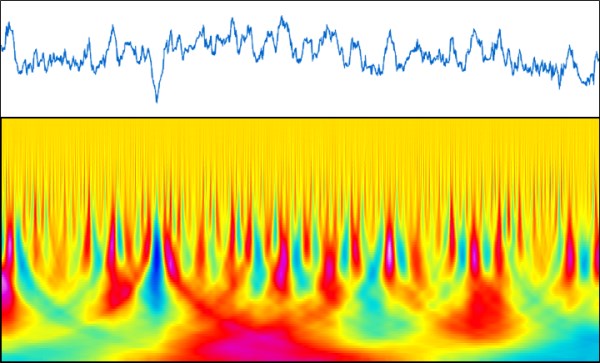
Beispiel einer Kontinuierlichen Wavelet-Transform (Continuous wavelet transform, CWT) auf einem Profil. Kurze Skalen oben, und große Skalen unten. Das Bild zeigt, dass auf unterschiedlichen Skalen unterschiedliche Strukturen und Merkmale sichtbar sind.
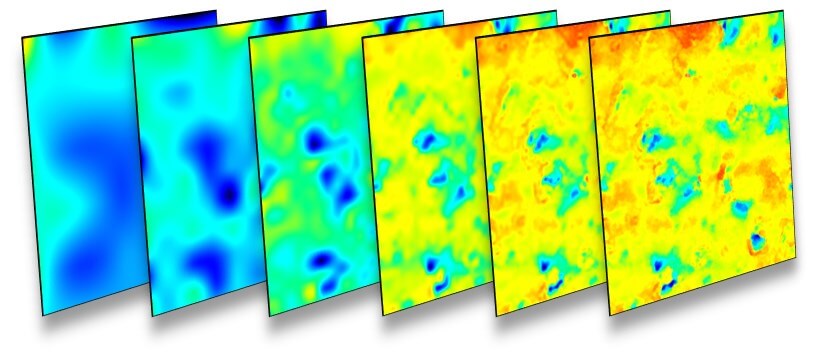
Oben: eine Oberfläche wird mit einem Diskreten Spline-Wavelet-Filter zerlegt. Jedes Bild wird aus den Skalierungsebenen oberhalb eines Schwellenwertes rekonstruiert, von 2 (links) bis 7 (rechts). Große Skalen sind auf der linken Seite. Das Bild rechts enthält alle Skalen.
Diese Funktionen sind im Modul Fourier & Wavelets Analyse für 3D-MountainsMap-Produkte enthalten, und im Modul 2D Advanced Surface Texture für 2D-MountainsMap-Produkte.
Randeffekte
Filter können entweder über Konvolution oder Fourier-Transformation (meistens FFT) implementiert werden. Im ersten Fall kann die Filtermatrix nicht bis zu den Ränder filtern, und die Hälfte der Matrix-Größe bleibt ungefiltert. Im letzten Fall führen Spektrum-Überlappungs-Probleme bei der Anwendung der FFT zu Rauschen an den Endportionen der gefilterten Daten. Aus diesen Gründen ist es üblich, einen Teil des gefilterten Profils (oder der gefilterten Oberfläche) an den Enden abzuschneiden. Jedoch beschreibt bis jetzt keine Norm, wie groß der abzuschneidende Teil sein soll. Einige Instrumentenhersteller haben beschlossen, zwei mal einen halben Cut-off (an beiden Enden) abzuschneiden, andere einen ganzen. In MountainsMap kann die zu entfernende Portion in den Grundeinstellungen für jeden Filtertyp gewählt werden.
[ISO 16610-28] beschreibt mehrere Optionen zum Umgang mit Randeffekten, so dass die gefilterten Daten den Profilen/Oberflächen in ihrer gesamten Größe entsprechen. Bei einigen Methoden wird eine Änderung der Filterfunktion nötig, wenn sie sich den Rändern annähert. Andere Methoden erweitern die Daten auf künstliche Art und Weise vor dem Filtern, bevor sie dann die gefilterten Daten kürzen, wodurch diese wieder die ursprüngliche Größe erreichen.
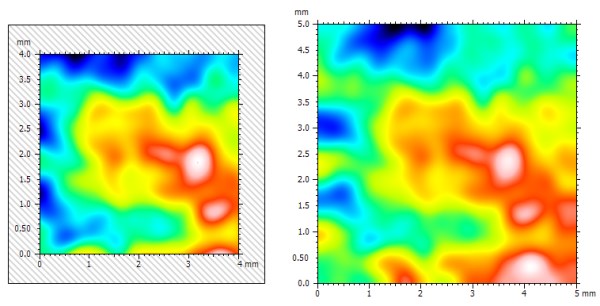
Oben: eine 5 mm x 5 mm große Oberfläche, gefiltert mit einem 1 mm großen Cut-off-Filter. Links: 36% der Fläche werden abgeschnitten. Rechts: Die gesamte Oberfläche wird beibehalten.
Morphologische Filter
Ein morphologisches Filter basiert auf zwei morphologische Operationen, Dilatation und Erosion, die mit einem strukturierenden Element einer bestimmten Größe arbeiten. Das Profil unten wird zum Beispiel über eine Scheibe mit einem bestimmten Radius ausgedehnt.

Die Scheibe rollt über die Oberfläche und der Weg ihrer Mitte wird aufgezeichnet (rote Linie). Dilatation (Ausdehnung) neigt dazu, Spitzen zu vergrößern und Löcher zu füllen. Strukturierende Elemente können theoretisch jede beliebige Form haben. Wenn die Scheibe unter der Oberfläche entlang gerollt wird, wird der Vorgang Erosion genannt.
Wenn zuerst eine Dilatation und dann eine Erosion durchgeführt wird, nennt man den Vorgang morphologisches Schließen; es handelt sich um ein morphologisches Filter, das eine obere Hülle erstellt. Die Scheibe wird unterhalb der Dilatationslinie gerollt. Die Hülle schließt Löcher und Poren, während sie den oberen Formen (Gipfel und Hügel) folgt.

Wenn die Sequenz umgekehrt wird, d.h. wenn zuerst eine Erosion und dann eine Dilatation durchgeführt wird, wird dieser Vorgang als morphologische Öffnung bezeichnet, die eine untere Hülle erzeugt.
Morphologische Filter sind in ISO [16610-41] für Profile und [ISO 16610-81] für Oberflächen beschrieben.
Die Anwendung eines morphologischen Filters ermöglicht es, eine Oberfläche im Bezug auf ihre Hülle zu verebnen. Folgendes Beispiel zeigt eine Oberfläche (links) mit Partikeln, die nicht auf einer ebenen Basis liegen, wodurch das Setzen eines Schwellenwertes erschwert wird. Wenn die untere Hülle berechnet wird, und von der Oberfläche abgezogen wird, wird der Sockel der Oberfläche verebnet.
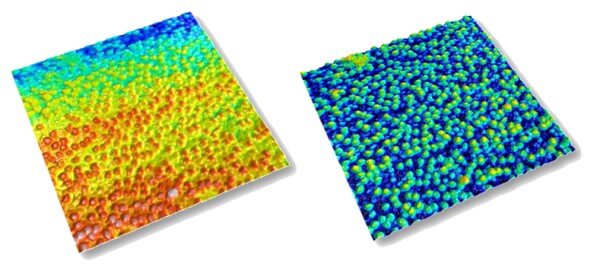
Wenn die Oberfläche mit Hilfe der oberen Hülle ausgerichtet werden würde, dann würden alle Partikelspitzen auf der gleichen Ebene liegen.
Morphologische Filter können auch als Filterkette verwendet werden, um eine Mehrskalen-Analyse durchzuführen. Diese Anwendung ist in [ISO 16610-49] für Profile und [ISO 16610-89] für Oberflächen beschrieben.
Morphologische Filter sind als Operator im optionalen Modul 3D Advanced Surface Texture erhältlich, und sind in den Software-Versionen MountainsMap SEM und MountainsMap Premium enthalten.
Filter zum Entfernen von Ausreißern
Optische Profilometer (Konfokale, Interferenz- und Fokusvariations-Profilometer) werden immer beliebter. Sie sind genau, schnell und können manchmal zusätzlich zur Höhenkarte ein Bild liefern. Sie haben jedoch folgenden Nachteil: sie erzeugen Ausreißer, d.h. Spikes, die nicht auf dem eigentlichen Werkstück sind.

Um diese optischen Geräte benutzen zu können, muss das Licht des Werkstückes auf dem Detektor reflektiert werden. Die Zeichnung oben zeigt auf der horizontalen Achse die Stärke des Signals am Detektor. Wenn das Signal gut genug ist (rechts), kann die Erfassungssoftware die Höhe korrekt und genau berechnen. Wenn kein Signal zum Detektor zurückgesendet wird (links), z.B. wenn das Messstück zu dunkel ist, oder wenn das Signal außerhalb des Objektives reflektiert wird, dann ist es unmöglich, eine Höhe zu erhalten; das Gerät erzeugt dann nicht gemessene Punkte, oder fehlende Punkte. Am problematischsten wird es dann, wenn ein Signal erkannt wird, dieses aber nicht deutlich genug ist, um eine korrekte Berechnung zu ermöglichen (schlechtes Signal-Rausch-Verhältnis), und das Gerät daher falsche Werte liefert, die viel höher oder niedriger als die Umgebung sein können. Diese Punkte werden Ausreißer genannt.
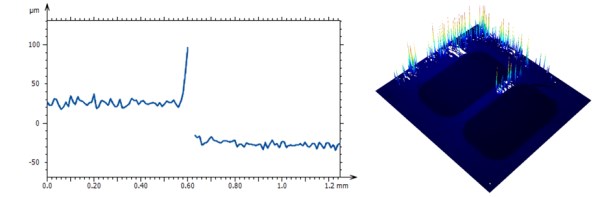
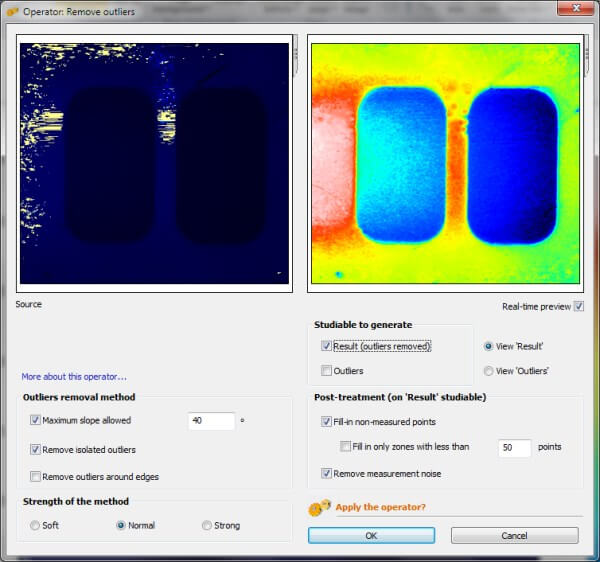
MountainsMap bietet ein spezielles Werkzeug, um Ausreißer automatisch zu erkennen, zu entfernen und dann die resultierenden nicht gemessenen Punkte auszufüllen.
Die Software bietet eine Kombination von Filtern, von denen jeder auf einen bestimmten Fall spezialisiert ist: isolierte Ausreißer oder Bänder von Ausreißern an einer Kante. Es ist auch möglich, eine maximale lokale Steigung zu definieren. Nicht gemessene Punkte werden dann mit einer glatten Form ausgefüllt, und ein letzter Glättfilter kann angewendet werden, um saubere Bilder für die Anzeige zu erzeugen.
Dieses Tool ist Teil der Software-Versionen MountainsMap Imaging Topography, MountainsMap Universal unt MountainsMap Premium, sowie Teil des Moduls 3D Advanced Surface Texture
FFT-Filter
Erweitertes Filtern kann durch direkte Edition des Fourier-Spektrums durchgeführt werden, das über die direkte Fourier-Transformation erhalten wird. Ein herkömmliches Filter wird üblicherweise über FFT implementiert, durch Multiplikation des Fourier-Spektrums mit der Gewichtungsfunktion des Filters, und danach durch Berechnung der inversen Fourier-Transformation. Das Fourier-Spektrum kann auch lokal von Hand oder mit Schwellenwerten bearbeitet werden, um spezifische Spektralspitzen oder Richtungen zu entfernen.
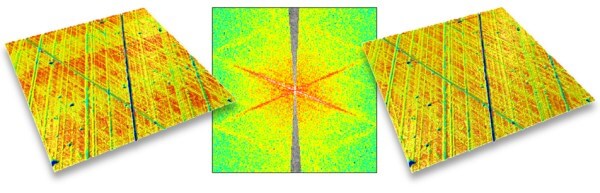
Oben weist eine mit einem 3D-Stylus-Profilometer gemessene Fläche Störungen auf, die aus Streifen bestehen, die eine Ebenenheitsabweichung aufweisen; diese wurden durch mangelhafte Geradheit des Y-Achsen-Tisches verursacht. Dieses Problem wird korrigiert, indem die entsprechende Richtung aus dem Spektrum (der Spektrumsmitte) entfernt wird, und indem die Oberfläche ohne diese Bänder wieder rekonstruiert wird (rechts)

Dieses zweite Beispiel zeigt, dass es sogar möglich ist, Kratzer in nur einer Richtung zu entfernen, um die andere Richtung separat zu analysieren.
FFT-Filter sind Teil des Moduls Fourier & Wavelets Analysis, und Teil der Software-Version MountainsMap Premium.
Normenreihe ISO 16610
ISO 16610 ist die Referenz-Norm für Profilfilter und Flächenfilter für Oberflächenbeschaffenheit und Formabweichungen. Bei der ersten Gruppe handelt es sich um Profilfilter, bei der zweiten Gruppe um Flächenfilter.
Grundlagen
Profilfilter
Flächenfilter
Hinweis: Profilfilternormen wurden zunächst als Technische Spezifikationen veröffentlicht. Sie werden nun schrittweise in internationale Normen umgewandelt. Die neuen Flächennormen werden direkt als Internationale Normen veröffentlicht.
WD: Working Draft (Arbeitsentwurf), CD: Committee Draft (Ausschussentwurf), DIS: Internationaler Normenentwurf, FDIS: Internationaler Normenschlussentwurf, TS: Technische Spezifikation.
Diese Seite kann als PDF-Artikel heruntergeladen werden: Bewährte Methoden für den Einsatz von Flächenfiltern.
Nächste Seite Internationale Normen zur Oberflächenbeschaffenheit