Filtration is required for several purposes in the process of surface texture analysis. A morphological filter is commonly used to correct the stylus tip effect on raw data; an outliers removal filter may be needed to clean up data measured with an optical probe. In some cases, a smoothing filter, such as a λs or S-Filter, is required to compare data measured with different instrument methods. But the main reason for using a filter is to separate long-scale components from short-scale components, in other words to separate waviness from roughness, and calculate parameters according to the specification.
1. Filtration scheme
With the replacement of former profile standards by ISO 21920, the filtration scheme for profiles is changed and a new vocabulary is introduced. The same operations are applied but the order between the S Filter and the F Operation is inverted. It may sometimes generate small differences in the parameter values, especially when profiles have large slope or form.
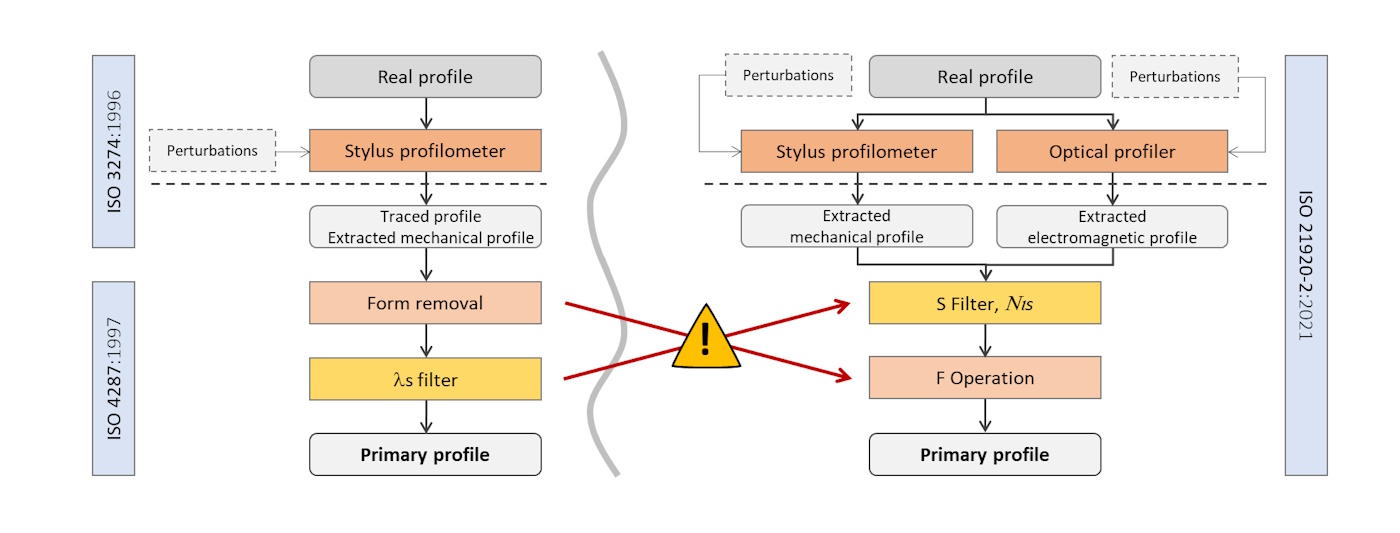
Before 2021, the ISO 3274 standard defined the measurement workflow as shown above on the left. The profile, measured by a profilometer is now digitized. It is called the extracted profile. It is sampled in X and digitized in Z and it represents an abstraction of the real surface (several filters occur during the measurement due to the limited bandwidth of the instrument). The real surface of the measured workpiece can be imagined by mechanical surface (envelope), when measured with a stylus profilometer, or by an electromagnetic surface, that represents the interface seen by an optical sensor (which characteristics are different between different optical techniques). To produce the primary profile that is the starting point of the metrological analysis, we need to apply a form removal and apply a λs filter (S Filter) that removes the microroughness. These two operations are not applied in the same order between the old and new standards. And sometimes, the S Filter is omitted, as in the German VDA 2006 standard used in the automative industry.
The workflow for surfaces, according to ISO 25178-2, is similar, by replacing the real profile by the real surface, and the primary profile by the primary surface.
Parameters are then calculated from the primary profile (or primary surface), or by applying additional S or L filters. The following workflow shows the difference of process between profiles and surfaces, and in particular, the fact that the primary surface still contains form, contrary to the primary profile, for historical reasons.
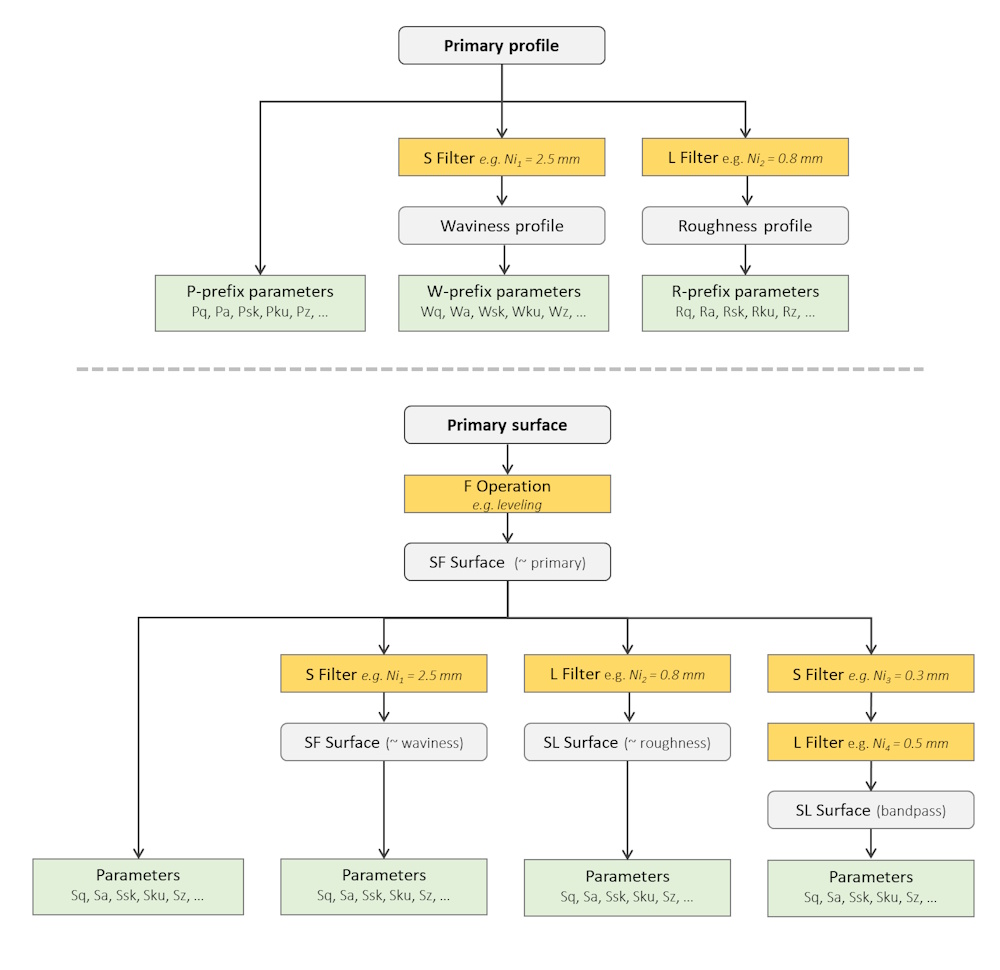
In reality, the L Filter is obtained by subtracting the waviness profile (or surface) from the primary profile (or surface). That is why they use the same cut-off. But during the analysis of a workpiece, it is possible to have roughness and waviness calculated with different cut-offs, if that is justified in a functional point of view. Profile parameters are then calculated according to ISO 21920-2, and surface parameters are calculated according to ISO 25178-2.
2. Vocabulary
The new vocabulary initially introduced for surfaces in ISO 25178 was later adapted to profiles in ISO 21920:
S Filter: filter that attenuates short wavelengths (S for short). It is a smoothing filter, used either to remove the microroughness (with a small cut-off), or to create waviness (with the main cut-off).
L Filter: filter that attenuates long wavelengths (L for long). This filter is obtained by the difference between the primary and the waviness profile (or surface), with the main cut-off.
F Operation: operation that removes the form or slope. Review the various F operation methods.
SF Surface: surface obtained by applying a S Filter and a F Operator.
SL Surface: surface obtained by applying a S Filter and a L Filter.
Primary surface: surface obtained by applying a S Filter.
Nesting index: is either a cut-off for a linear filter, or the size of a structuring element for a morphological filter, or the Wolf pruning threshold for the watersheds segmentation. Nesting index is a generic term for the criterion that tunes the filter strength.
Primary profile: profile filtered with a S Filter (λs) and with form removed by a F Operator. It is the equivalent of an SF profile.
Waviness profile: profile filtered with a S Filter (λc) to only keep long wavelengths. It is also the equivalent of an SF profile, with another cut-off.
Roughness profile: profile filtered with a L Filter (λc) to only keep short wavelengths. It is the equivalent of a SL profile (The S Filter comes from the primary profile).
3. Historical filters
The first filters were implemented as physical high-pass filters using resistors and capacitors soldered behind a selector. The initial aim was to avoid large signal variations in order to draw the profile correctly on a thermal band of paper, or to display a roughness average indication on a dial indicator. These RC filters were used for almost 30 years on all types of stylus profilometers. In the 1980's, personal computers started to be used as analysis devices connected to profilometers via analog-to-digital boards. The first profile analysis programs implemented the RC filter using an algorithm in order to provide the same amount of filtering as the analog filter.
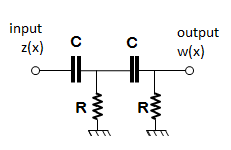

Analog RC2 filter (left) and Talysurf 10 with cut-off selection (right)
The major drawback of this filter is the phase distortion of its transfer function. Each wavelength in the original profile is shifted by a different amount leading to critical problems around steps, grooves and peaks.
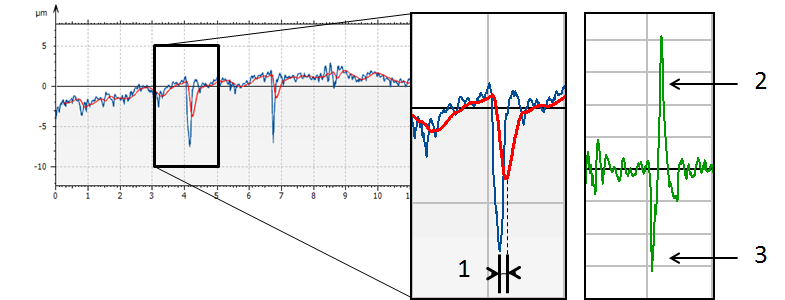
Analog RC2 filter
Above: a close look at the phase shift (1) effect on a groove. The mean line is "late" compared to the primary profile. On the roughness profile, this produces amplified peaks at the location of the groove (2) and minimized groove depth (3).
At the beginning of the 1990's, a phase-correct version of the RC2 filter was created in an attempt to fix this problem. It was called RC2-PC. However, more serious work was already underway to produce a natively phase correct filter, the Gaussian filter.
Introduction to filtration
This video introduces the bases of filtration in surface texture and explains how filters act on the spectral content of profiles and surfaces. Durée : 19 min 57.
4. Gaussian filters
The Gaussian filter was introduced, for profiles, in the [ISO 11562] standard in 1996. The standard defines a transfer function for the low-pass filter that produces the waviness (mean line) profile. Subtracting this mean line from the primary profile gives the roughness profile.
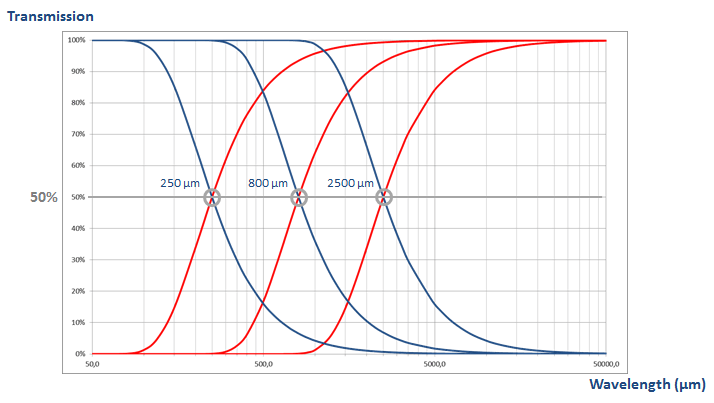
Transmission characteristics for the roughness filter (blue) and waviness filter (red), for several cut-off values. These curves cross each other at 50% of transmission.
It is a common practice to cut each end of the filtered profile by a length depending on manufacturers. Some cut half a cut-off at each end, others cut a full cut-off. In theory, the value should be at least 0.6 cut-off. The consequence is that the roughness or waviness profile is shorter than the primary profile by 1 cut-off or 2 cut-offs.
In MountainsMap, users can select the length which is cut out from the filtered profile, and can also activate an option to manage end-effects in order to keep the full length.
In 2011, [ISO 16610-21] became the official standard defining the Gaussian filter for open or closed profiles, replacing the old ISO 11562. For surfaces, the equivalent definition is given in [ISO 16610-61].
More details on areal filters can be found in [SEEWIG 2013]
At the cut-off value, the filter transmits (attenuates) 50% of wavelength's amplitude. Filters should not be seen as shutters that block wavelengths suddenly; The transmission characteristics are continuous and progressive. Therefore, the choice of the cut-off value is critical, depending on the application, in order to correctly separate wavelengths (or scales) that belong to the surface texture component of interest.
Gaussian filters have been successfully used for various applications in industry and research for 20 years. However, this filter does not behave very well around outliers, steps and in the presence of form. This is why robust filters have been developed.
5. Robust Gaussian filters
A robust filter has its mean line (plane) correctly following the general trend of the profile (surface), without being disturbed by outliers. The Robust Regression Gaussian Filter is defined in [ISO 16610-31] as an iterative algorithm that calculates local weights based on the distance between the primary profile and the waviness profile.

The Gaussian filter (left) is disturbed by local discontinuities while Robust Gaussian filter (right) is not.
The Robust Gaussian filter is the preferred choice for structured surfaces, stratified surfaces and in presence of form, grooves or pores. In particular, it is a good replacement for and improvement on the double Gaussian filter that is defined in [ISO 13565-1] (formerly DIN 4777)
6. Cut-off vs Nesting index
The term cut-off is used today for defining the wavelength at which the filter attenuates the amplitude by 50%. It also means that this wavelength is transmitted at 50%. Users should select the cut-off value wisely in order to separate two wavelength populations and, for example, not cut right in the middle of one of the populations. In other words, if the workpiece contains roughness and waviness, the spectrum will show a population of wavelengths for roughness and another one for waviness. The cut-off value should be specified so that it separates the two populations without distorting them. In some cases, the workpiece is flat enough and there is no waviness; in such a case the filter is not required.
For profiles, cut-off values should be selected from a series described in [ISO 4288]: ... 0,08 mm; 0,25 mm; 0,8 mm; 2,5 mm ...
However, users who analyze workpieces that fall outside the scope of the GPS system (which is primarily concerned with mechanical components) may choose other cut-off values. In such a case, the user should carry out a functional correlation test in order to establish correspondence between the filter type and cut-off value on one hand and the performance of the function that is being monitored on the other. For example, steel sheets may be filtered with a cut-off of 5 mm to isolate the waviness which is printed on the sheet by vibrating rollers.
For surfaces, the recommended series of cut-off values is described in [ISO 25178-3]: ... 0,1 mm; 0,2 mm; 0,25 mm; 0,5 mm; 0,8 mm; 1,0 mm ...
The term nesting index was forged to widen the concept of cut-off which is only applicable to linear filters. In the ISO 16610 Series, new filters are defined that are not linear filters, such as the Morphological filter and the Robust Spline filter. Hence the term cut-off cannot be used for these filters and the term nesting index is used instead. A nesting index is a parameter value that controls the filter and the way it separates scales or wavelengths.
For a Spline filter, the nesting index is just the cut-off. For a morphological filter, the nesting index is the shape of the structuring element (e.g. sphere) and its size (diameter).
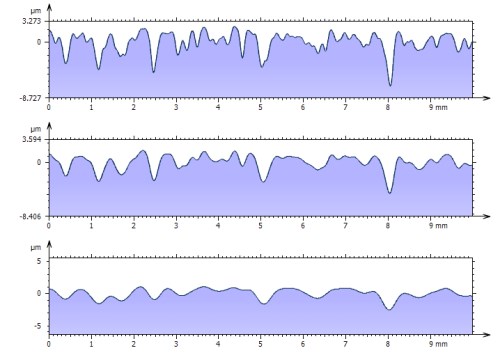
Filtered profiles (waviness) with different cut-offs
(from top to bottom: 0,2 mm, 0,4 mm and 0,8 mm)
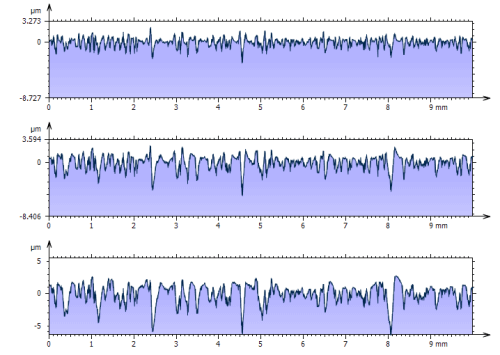
Filtered profiles (roughness) same cut-offs as above.
7. Cubic Spline filters
Cubic splines are geometrical curves that smoothly link a series of points. Splines are used to draw curved shapes in CAD programs and are also used to interpolate data points.
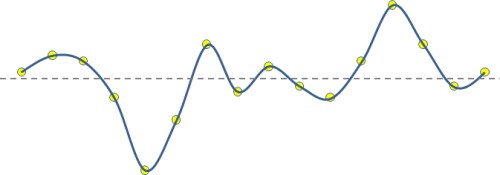
Data points (yellow) connected by a Spline curve (blue).
After the application of a cubic spline filter, the spline curve does not pass through data points but through suspended points. These points are connected to data points with a spring characterized by a spring constant β which is called the tension parameter. Setting this spring constant (to a value between 0 and 1) makes it possible to control the behavior of the filter.

Suspended points (green) connected to the original data points by an elastic spring. The spline curve (blue) now represents the filtered profile (waviness).
By default (with β = 0.6252) the behavior of the Cubic spline filter is very close to the Gaussian filter.
The Cubic spline filter is described in [ISO 16610-22] for profiles and in [ISO 16610-62] for surfaces.
In practice, the spline filter does not have significant advantages over the Gaussian filter.
8. Robust Spline filters
A variant was designed in order to bring robustness to the definition of the Spline filter. The Robust Spline filter is defined in [ISO 16610-32] for profiles and [ISO 16610-62] for surfaces. Due to its non-linear nature, its implementation is quite complex and this filter is not commonly found in analysis software.
Although this robust filter is theoretically better than the Robust Gaussian filter, the results are very close in both cases and as the Robust Gaussian filter is much simpler to implement, it is preferred in most cases.
9. Wavelets filters
Wavelets filters are based on localized harmonic analysis using short-term signals called mother wavelets. In surface texture applications, wavelets filters are used to decompose profiles and surfaces into different scales. This makes it possible to identify a particular scale at which a phenomenon occurs, and also to remove a feature at a particular scale and reconstruct the signal without that feature (outlier or structure).
Wavelets filters are defined in [ISO 16610-29] for profiles and [ISO 16610-69] for surfaces. For the moment, only Spline wavelets are defined in the standard. Complex wavelets should be added in the future, especially for surfaces. The literature describes a lot of other types of wavelets (Coiflet, Daubechies, ...) that are used in specific applications such as infrared image analysis or earthquake signals, but that are less interesting in surface texture.
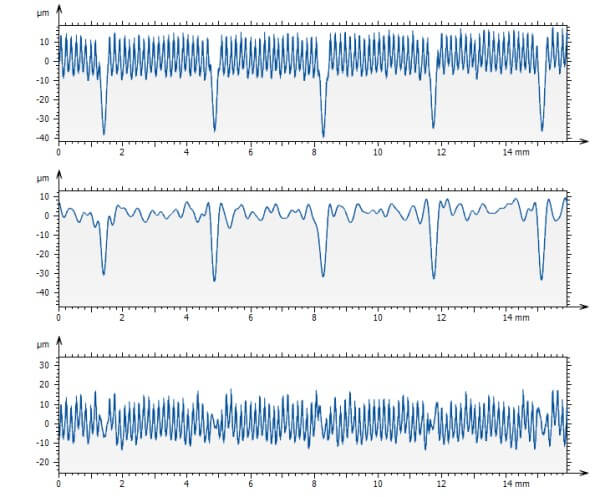
Above: a profile that contains two superimposed periodic structures is filtered by a Discrete Wavelets Filter using a Meyer wavelet. The two signals are clearly separated for further analysis.
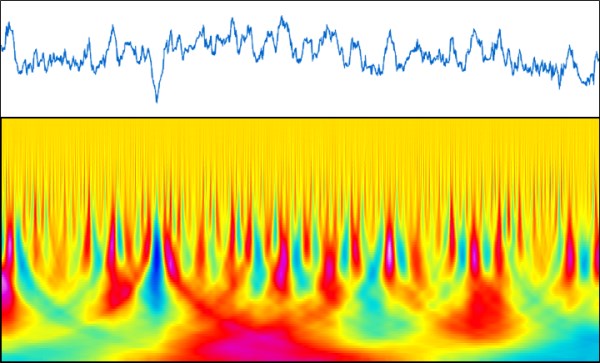
Example of a continuous wavelets transform (CWT) on a profile. Short scales are at the top and large scales at the bottom. The image shows that different structures and features are visible at different scales.
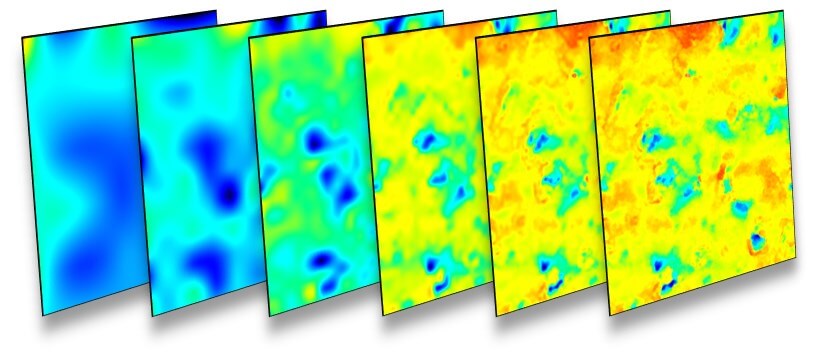
Above: a surface is decomposed using a Discrete Spline Wavelet Filter. Each image is reconstructed from the levels of scales above a threshold, from 2 (left) to 7 (right). Large scales are on the left. The image on the right contains all scales.
These features are available in the Fourier & Wavelets Analysis module for 3D MountainsMap products and in the Advanced Profile module for profilometry Mountains® products.
10. End-effects
Filters can be implemented either by convolution or by Fourier Transform (usually FFT). In the former case, the filter matrix cannot filter up to the edges and half of the matrix size is left unfiltered. In the latter case, spectrum overlapping during the application of the FFT diverges at the edges of the filtered data. For these reasons, it is a convention to cut out a portion of the filtered profile (or surface). However, no standard has ever specified the amount of cut-out. Some instrument manufacturers used to cut out half the size of the cut-off at both edges, others cut out one full cut-off. In MountainsMap, this amount can be selected in the Preferences, for each filter type.
[ISO 16610-28] describes several options for dealing with end-effects so that the filtered data retains full size profiles/surfaces. Some methods require modification of the filter function as it approaches the edges. Other methods artificially extend the data before the filtration, then cut out the filtered data which comes back to the original size.
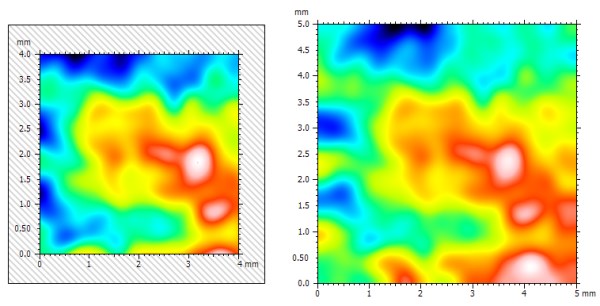
Above: a 5 mm x 5 mm filtered with a 1 mm cut-off filter. Left: 36% of the area is cut-out. Right: the full surface is kept.
11. Morphological filters
A morphological filter is based on two morphological operations, dilation and erosion, that work using a structuring element of a given size. For example, the profile below is dilated by a disk of a certain radius.

The disk rolls over the surface and the path of its center is recorded (red line). Dilation tends to enlarge peaks and fill holes in. Structuring elements can be theoretically of any shape. If the disk is rolled below the surface, it is called an erosion.
When dilation is followed by erosion, it is called a morphological closing which is a morphological filter that creates the upper envelope. The disk is rolled below the dilation line. The envelope closes holes and pores while following the upper shapes of peaks and hills.

If the sequence is reversed, i.e. erosion followed by a dilation, it is called a morphological opening which creates the lower envelope.
Morphological filters are defined in [ISO 16610-41] for profiles and [ISO 16610-81] for surfaces.
An application of morphological filters is the ability to flatten a surface with respect to its envelope. The following example shows a surface (left) with particles that are not seating on an even base, making it difficult to threshold. When the lower envelope is calculated and subtracted from the surface, the bulk of the surface is flattened.
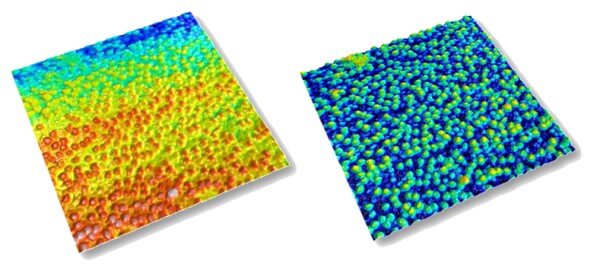
If the surface were leveled using the upper envelope, all particles would have their summit aligned on the same plane.
Morphological filters can also be chained in order to create a bank of cascading filters and carry out a multiscale analysis. This application is described in [ISO 16610-49] for profiles and [ISO 16610-89] for surfaces.
Morphological filters are available as an operator in the Advanced Topography optional module and are included in MountainsMap® SEM and in MountainsMap® Premium.
12. Outlier removal filters
Optical profilers, either confocal, interferometric or focus variation, are becoming more and more popular. They are accurate, fast and sometimes can also provide an image in addition to the height map. However, they have a drawback: they generate outliers, i.e. spikes that are not on the actual workpiece.

These optical devices require the light to be reflected from the workpiece onto the detector. The drawing above represents on the horizontal axis the strength of the signal on the detector. When the signal is good enough (right), the acquisition software is able to calculate the height correctly and accurately. When no signal at all is coming back onto the detector (left), for example if the sample is too dark or if it reflects the signal outside the objective, then it is impossible to get a height and the device produces non-measured points, or missing points. The main problem arises when some signal is detected but not enough to allow a correct calculation (bad signal-to-noise ratio), hence the device provides incorrect values which may be much higher or lower than the surrounding area. These points are called outliers.
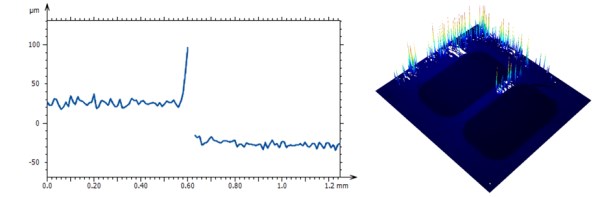
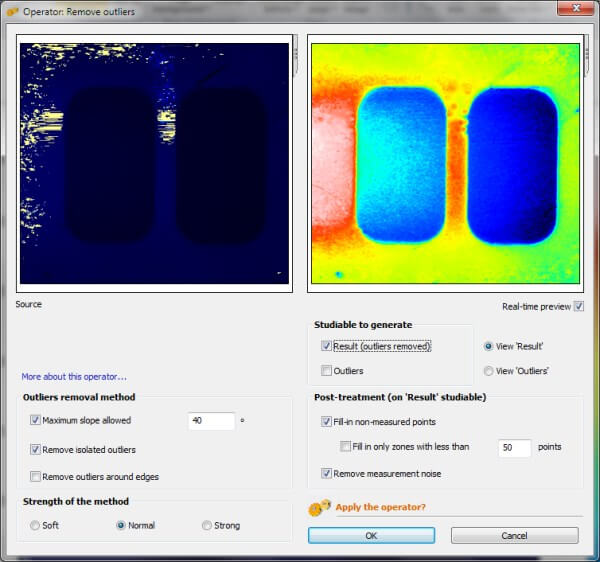
MountainsMap offers a dedicated tool to automatically detect outliers, remove them and then fill in the resulting non-measured points.
It provides a combination of filters, each of them targeting a specific case: isolated outliers or bands of outliers around an edge. It is also possible to set a maximum local slope. Non-measured points are then filled in with a smooth shape and a final smoothing filter can be applied in order to produce clean images for display.
This tool is included in MountainsMap® Imaging Topography and MountainsMap® Premium, as well as in the Advanced Topography module
13. FFT filters
Advanced filtering may be carried out by directly editing the Fourier spectrum which is obtained by direct Fourier transform. A traditional filter is usually implemented using the FFT, by multiplying the Fourier spectrum by the weighting function of the filter, then calculating the inverse Fourier Transform. The Fourier spectrum may also be edited locally by hand or using thresholds, in order to remove specific spectral peaks or directionalities.
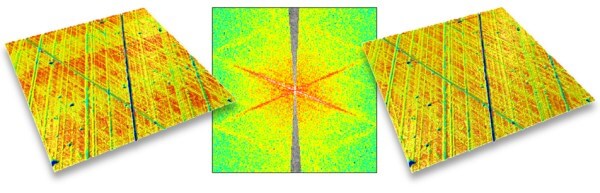
Above, a surface measured by a 3D stylus profilometer is altered by flatness deviation bands due to incorrect straightness of the Y-axis stage. This problem is corrected by removing the corresponding directionality from the spectrum (center) and reconstructing the surface without the bands (right)

This second example shows that it is even possible to remove scratches in only one direction in order to analyze the other direction separately.
FFT Filters are included in the Fourier & Wavelets Analysis module and in MountainsMap® Premium.
14. ISO 16610 Master Plan
ISO 16610 is the reference standard for profile and areal filters for surface texture and form deviation. The first group of parts covers profile filters, the second group covers areal filters.
General Concepts
Profile Filters
Areal Filters
WD: Working draft, CD: Committee draft, DIS: Draft international standard, FDIS: Final draft international standard, IS: International standard (published), TS: Technical specification, TR: Technical report
Next page: International Standards for Surface Texture
