What is a bandpass filter?
The combination of a high-pass filter and a low-pass filter may be used to establish a narrow bandwidth which can help to study surface behavior at a particular scale. It is therefore another way to do multiscale analyses of profiles and surfaces. Here are some explanations on this type of filtering, and how it is implemented into Mountains®.
1. The concept of bandpass in surface analysis
Roughness and waviness are two convenient names to designate scale-limited profiles.
A waviness profile is filtered using a low-pass filter, which means that low frequencies (long wavelengths) pass and high frequencies (short wavelengths) are attenuated.
A roughness profile is obtained by the opposite process, using a high-pass filter which attenuates long wavelengths.
Each of these profiles receives a subset of the frequencies contained in the original profile. In this sense, they are band-limited, or scale-limited.
When both low-pass and high-pass filters are applied consecutively with the same cut-off value, wavelengths below and above the cut-off are attenuated and only the wavelengths around the cut-off value are transmitted.
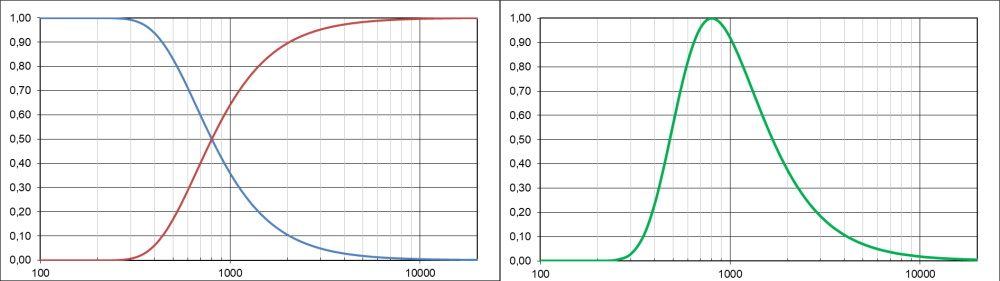
Left: Classic Gaussian transmission characteristics for a cutoff of 800μm (blue curve for roughness, red one for waviness). Right: Combined transmission characteristics, compensated with a factor 4, form the elementary bandpass filter. Transmission is on the vertical axis, wavelengths on the horizontal axis, in μm.
Both types of filters have a transmission factor of 50% at the cut-off, so the transmitted wavelength is transmitted at 25%. By construction, this factor can be compensated by multiplying the result by 4 to obtain a transmission of 100% at the cut-off. This is what is done in the VDA2007 standard to detect dominant wavelengths.
This type of filter is known as a bandpass filter. It isolates a narrow bandwidth at a particular cut-off and allows us to analyze the behavior of the surface at that scale. Sweeping the value of the central cut-off, from the smallest to the largest wavelengths, enables multi-scale analysis.
2. Symmetrical Gaussian filter
Due to the shape of the Gaussian transmission characteristics, the bandpass curve is non-symmetrical. This is due to the fact that roughness is in fact obtained by subtracting waviness from the original profile. However, in signal and audio processing, low-pass and high-pass filters are symmetrical by construction.
It is however possible to apply the same principles to surface analysis and obtain a symmetrical filter.
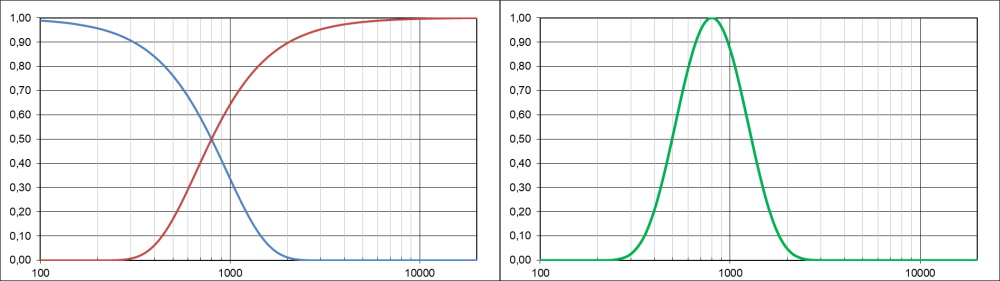
Transmission characteristics of a symmetrical Gaussian bandpass filter.
3. Filter bank
Multi-scale analysis using bandpass filters can generate a series of profiles or a series of surfaces, each filtered at a different cut-off value. This illustrates the concept of filter bank which decomposes the spectrum into individual bands, like an audio graphical equalizer. The number of scales can be defined by the number of bands per octave, an octave being the interval between a wavelength and its double or its half.
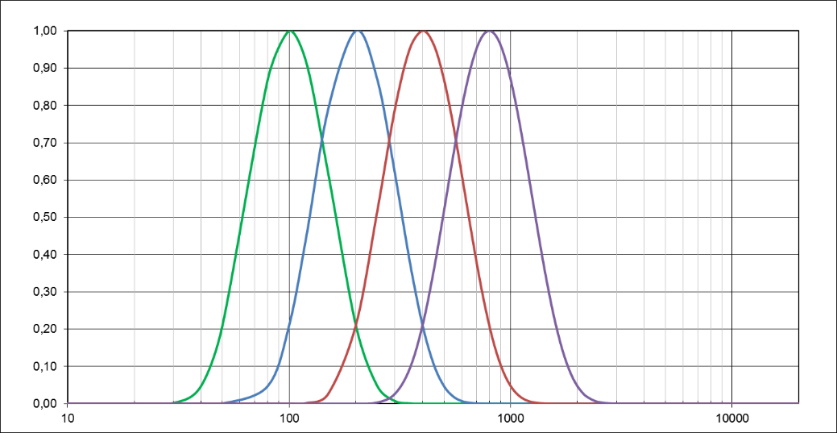
Four symmetrical bandpass filters centered at each octave.
Symmetrical filters can be cascaded to obtain second, fourth or eighth orders that have more selective transmission curves with less overlap. They can be used to decompose the spectrum into more bands.

Transmission characteristics of symmetrical Gaussian filters, of first order (green), second order (blue) and fourth order (purple).
About the term "octave"
The term octave is quite unusual in surface metrology but it is common in signal processing and even more in music. An octave is the interval between a (musical) note and the same note corresponding to the higher or lower harmonic. The physical meaning is the interval between a frequency and its double or its half.
Further information: Octave, in Wikipedia
4. New filter tool
The Bandpass-filter bank Operator that is available in Mountains® decomposes a profile or a surface into a series of bands that can then be analyzed using surface texture parameters. Functional correlation may be carried out to identify active bands, where correlation is higher. This can help in identifying the range of scales to be used to control a particular function on a workpiece.
The tool also provides a new way to perform multi-scale analysis, as an alternative to wavelet analyses or scale-sensitive fractal analyses (SSFA), both already available in Mountains®. Bandpass-filter banks have the advantage of using tools that are easier to understand, based on the well-known Gaussian filter.
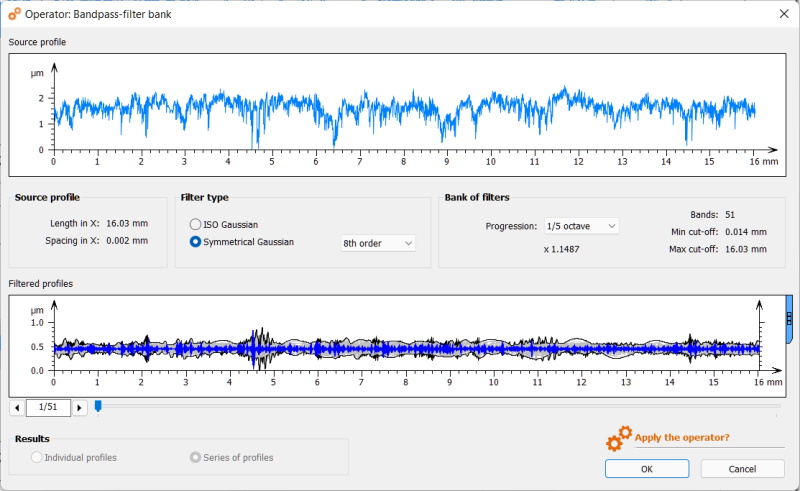
Mountains® offers a Bandpass-filter operator for surfaces and for profiles (above).
Physical phenomena are usually multi-scale in nature, so complex surfaces should be analyzed using multi-scale tools, to capture this complexity, and Mountains® software now offers a full range of these.
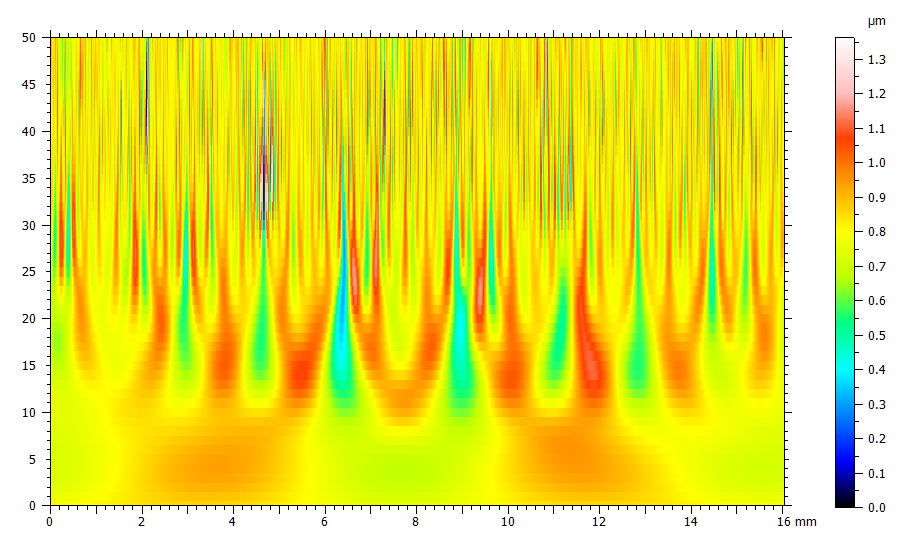
Example of multi-scale analysis on a profile, using a Gaussian filter bank. The series of profiles is converted to a surface (each line is a profile). It is similar to the continuous wavelets analysis.