Surface Texture on Freeform Surfaces


Most engineers and designers of mechanical components know roughness specifications through profile parameters, such as Ra. Many metrologists in the industry control surface texture specifications using a stylus profilometer that measures heights along a profile. This is fine as long as the texture is simple enough and homogeneous enough. But more and more, engineered surfaces have patterns, structures or specific texture printed, added or implanted on them, in order to better control surface function (adhesion, lubrication, hydrophobicity, …) Specifications on such surfaces are more reliable and representative if they use areal parameters calculated on surfaces. The introduction of areal surface metrology was an important turn around the 1990s.

However, the true complexity of a real surface may not even always be fully captured with a standard surface, coded on a matrix of heights. When the surface has complex form and small texture superimposed, or when the manufacturing process creates spatter particles or cavities, or when you are interested in characterizing roughness on the vertical wall of a rectangular trench, an acquisition along the Z-axis will result in lost information.

So, what’s the solution? Freeform surfaces are the next paradigm shift...


1. Towards a true surface representation

In order to keep the surface information intact during acquisition and analysis, it is necessary to move the data structure from a function z=f(x,y), where one height value is coded for every x,y position on a regular grid, to a curvilinear form, (x,y,z)=f(u,v), where points in space are connected to their neighbors as triangles.

A Freeform surface, called a Shell in MountainsMap®, is a point cloud (x,y,z) associated with connectivity information so that all points are connected in a triangle mesh in space. That way, the complete surface around an object can be coded. It also allows coding of undercut structures or internal cavities (see example image below).

3D View in MountainsMap® of a shell (or freeform surface) of metallic powder melted by a laser, Laser Powder Bed Fusion (LPBF) in additive manufacturing. Non-melted powder particles are visible above the surface, as well as a cavity below the surface. The triangle mesh and points have been overlapped on a colored surface.


Triangle meshes are commonly used in Dimensional Metrology to represent, for example, a mechanical workpiece measured by a Coordinate Measuring Machine (CMM). The difference here, is that its resolution has to be fine enough in order to allow surface texture analysis at a micrometer scale.

MountainsMap® is compatible with freeform data structures. The proposed features form the basis of an analysis ecosystem around Freeform surfaces (Shells) that can be used by advanced users, especially when using X-ray computed tomography instruments.


2. Acquisition of Freeform Surfaces

Freeform Surfaces can be produced by several instrumental techniques:

  • Optical profilometry (confocal, interferometer, focus variation…): multiple acquisitions are performed at different angles, then partial height maps (standard surfaces) are stitched together into a single mesh in space.
  • Scanning Electron Microscope (SEM): images are processed by pairs; reconstructed height maps are stitched together.
  • X-ray Computer Tomography (XCT): an interfacial surface extracted from a voxel cube.
  • µCMM or 3D Scanner: a point cloud of sufficient density is meshed into a Freeform surface under certain convexity conditions.


3. Freeform surface (shell) studiable

Mountains® can load Freeform Surfaces from various file formats (STL, 3MF, OBJ, PLY). They are loaded as Shell studiables and can be displayed in an interactive 3D View and further analyzed with Operators and Studies.

Besides coordinates and connectivity information, a Shell studiable may also contain additional information, called attributes, created during acquisition or extraction, or generated by a specific Operator in Mountains®. These attributes may be color or intensity values, normal vectors, distance values from the reference surface, or any application-oriented attribute that needs to be linked to the shell studiable. An attribute can be associated with points or triangles, or even edges.



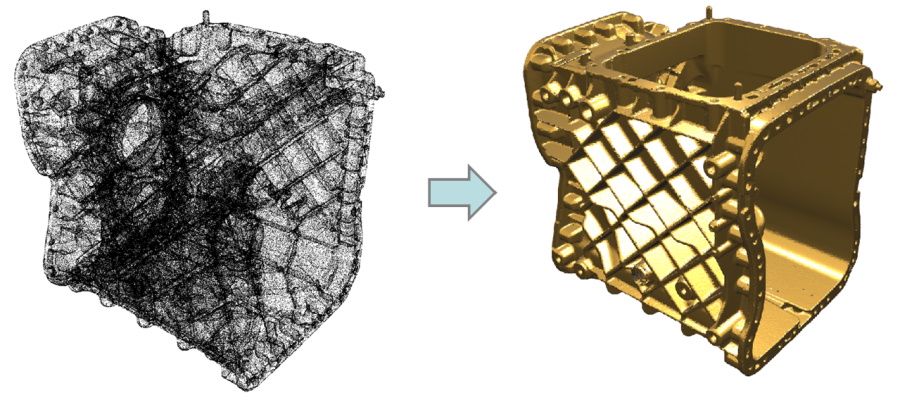
4. Meshing of a point cloud

When a workpiece is scanned as a point cloud, it is possible to reconstruct its surface as a shell, thanks to a fast and powerful algorithm based on the latest scientific publications. An automatic mode chooses the best meshing parameters for you, but it is still possible to tune them manually if you need for complex parts.

The meshing operator accepts point cloud of several millions of points.




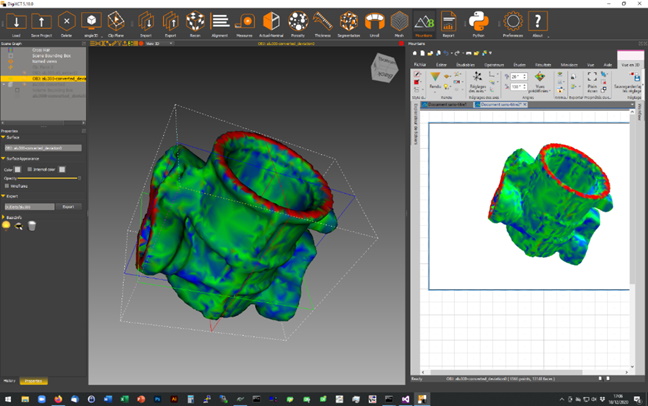
5. Extraction of a shell from a XCT data

A bridge between the DigiXCT® software from Digisens and Mountains® was developed. It offers a tight integration and a great ease of use. Digisens is specialized in the analysis of data measured by x-ray computed tomographs for inspection and metrology. DigiXCT is responsible for the 3D reconstruction from x-ray images, and the extraction of the shell surface from the density stored into the voxel cube. The shell is then send directly to Mountains® through memory interfaces for further analysis. The link to the original volume dataset is maintained over time, in case it is necessary to change the region of interest or the reconstruction parameters.



6. Conversion to a surface / Extraction of a contour profile

Mountains® includes two conversion operators

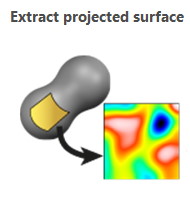
Extract Projected Surface This operator allows the user to orient the freeform surface and position a rectangle to define the portion of the freeform surface to extract and convert to a standard surface. Useful, for example, when analyzing roughness on an internal surface (e.g. the internal surface of the chamber of a pump produce by additive manufacturing that cannot be accessed by regular profiler unless the workpiece is cut)

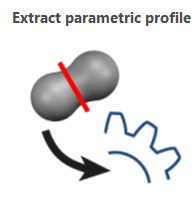
Extract Parametric Profile This operator intersects the freeform surface with an oriented plane in order to create a contour profile that can be analyzed in the Advanced Contour Study. This can be useful, for example, for checking angles and dimensions or even comparing the profile with a DXF model.

7. Correction et preparation of a shell

After a shell is loaded, it is usually necessary to apply some corrections to elimiate duplicated points or incorrect triangles. Moreover, it is the occasion to build internal data structures that allow a fast access to neighbour points (adjacency and incidency) and to calculate face and vertex normals.

Another important operation: the remeshing. This operator reduces the number of vertices (decimation) or increase them (subdivision), or homogenize faces making them quasi-equilateral (Delaunay condition). Finally an optimization of the mesh will reduce the density of faces in flat areas and keep the details where the local curvature is high.



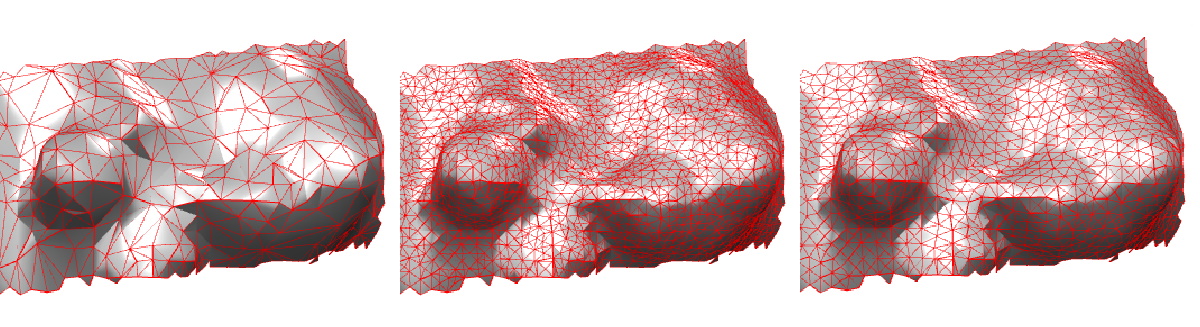
6. Surface texture parameters on a freeform surface

Digital Surf has been partnering with the Center of Precision Technologies at the University of Huddersfield (UK) to develop a set of surface texture parameters calculated on freeform surfaces. A team of talented researchers and PhD students at Huddersfield have developed the background mathematics and adapted the definitions of areal surface texture parameters to apply on freeform surfaces.

A symmetrical expression can be found for most parameters on freeform surfaces compared to standard surfaces:

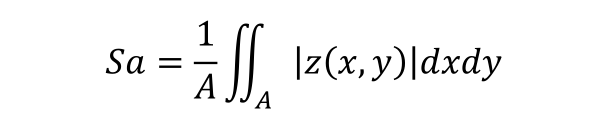Definition of Sa on a Standard Surface

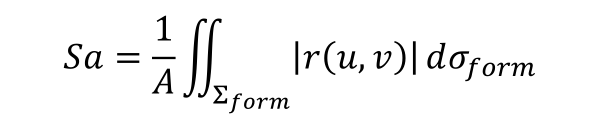Definition of Sa on a Freeform Surface

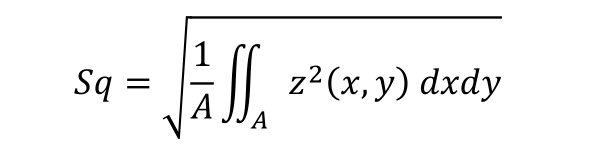Definition of Sq on a Standard Surface

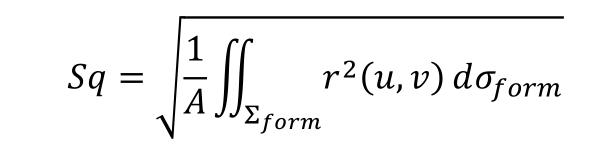Definition of Sq on a Freeform Surface


where Σform represents the form surface which acts as a reference surface from which the deviations r(u,v) are measured between each point of the Freeform surface and the form surface that is associated to it.

Mathematical details can be found in the paper:

Pagani L, Qi Q, Jiang XQ, Scott PJ, Towards a new definition of areal surface texture parameters on freeform surface, Measurement 2017.

A subset of the areal parameters have been converted for shells:

  • Sa, Sq, Ssk, Sku, Sp, Sv, Sz
  • Sdq, Sdr, Sdrp, Srf
  • Vm, Vv, Vmp, Vmc, Vvc, Vvv

Mountains® introduced the Shell Topography module that calculates a subset of ISO 25178-2 parameters directly on a loaded freeform surface, without the need to convert it to a standard surface. The parameters can be calculated on deviations from a geometrical form (plane, sphere, cylinder) or a filtered shell.



9. Form fitting

Parameters are calculated from the form deviation values associated with each point of the freeform surface. This means that a form surface has to be associated with the freeform surface. This is done by a dedicated plugin operator that fits a least-square form to the point cloud. The form can be a plane, polynomial, cylinder or sphere. It's a preliminary stage before parameters can be calculated.


Cylinder with deviation displayed with respect to the least-squares cylinder form.




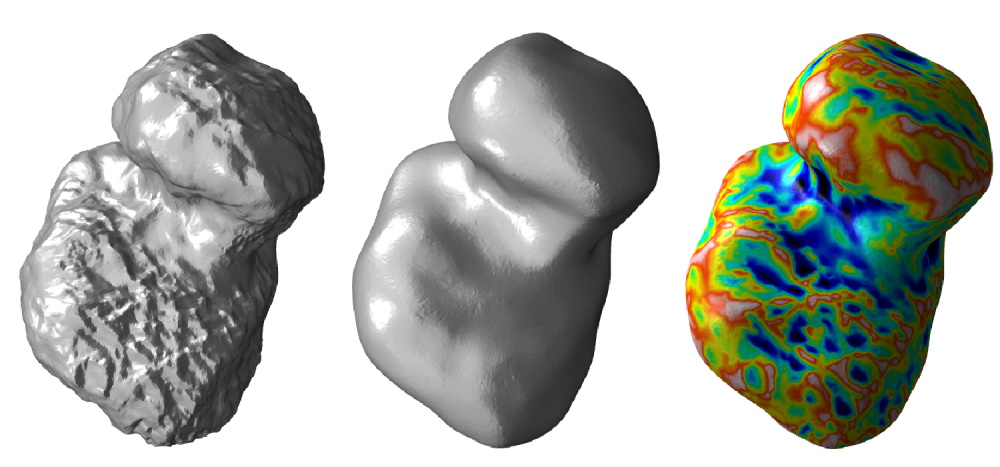
Left: the source shell, middle: the smoothed shell with a mean curvature flow filter, right: deviations between the two former shells, overlaid on the smoothed shell.

10. Filtration

In the case of a general shell that cannot be fitted with a geometrical form, it is then necessary to calculate a smooth version of the shell, similar to a waviness surface. Deviations are then calculated between the source and the smoothed shells.

Several filtration algorithms are available: a pseudo-Gaussian filter, a Bilatéral filter and a mean curvature flow filter.



11. Calculation of curvatures

Local curvature can be calculated using various algorithms (Stokely, Cohen-Steiner, Bousquet, Goldfeather) and combined differently: mean curvature, Gaussian curvature, or as indices such as curvedness or shape index. These attributes can be displayed on the 3D view as an overlay.




As a leader product for surface texture analysis, Mountains® embraces the next revolution in metrology and is committed to provide the tools necessary to users in Industry and Research. Initial feedback on these applications provided by users will help validate tools and prepare the forthcoming standardization.

You could say Digital Surf is preparing the future with key partners and some of this future is already available in Mountains®.



The book Freeform surfaces is the reference for the analysis of triangle mesh surfaces and is written by Professors Xianqiang (Jane) Jiang and Paul J Scott from the University of Huddersfield.

It covers the following subjects: Fundaments for Freeform Surfaces, Sampling for Freeform Surfaces, Freeform Surface Fitting, Linear and Non-linear Diffusion Filtration, Morphological Filtration, Wavelets Filtration, Segmentation of Features on Freeform Surfaces, Characterisation for Freeform Surfaces, Characterisation of Freeform Structured Surfaces, Freeform Surface Design and Metrology Platform.

Additional resources