Techniques de filtrage des états de surface
Le Filtrage est une opération requise pour plusieurs raisons en analyse des états de surface. Une filtre morphologique est couramment appliqué dans les profilomètres pour corriger l'effet du stylet sur le profil mesuré ; un filtre de suppression des points aberrants peut être nécessaire pour nettoyer les données mesurées par un capteur optique. Parfois, un filtre lissant ou débruiteur comme le filtre λs ou Filtre S, peut être nécessaire pour comparer des données issues d'instruments utilisant des techniques différentes. Mais la raison principale de l'utilisation d'un filtre reste la séparation des composants de grande longueur d'onde des composants à courte longueur d'onde, autrement dit de séparer ondulation et rugosité, afin de calculer des paramètres adaptés à l'application.
1. Schéma de filtrage
Avec le remplacement des anciennes normes sur les profils par la norme ISO 21920, le schéma de filtrage pour les profils a évolué, ainsi que le vocabulaire utilisé. Les mêmes opérations sont appliquées mais l'ordre entre le filtre S et l'opération F a été inversé. Cela peut parfois occasionner de petites différences dans les paramètres calculés, notamment sur les profils présentant une pente ou une forme.
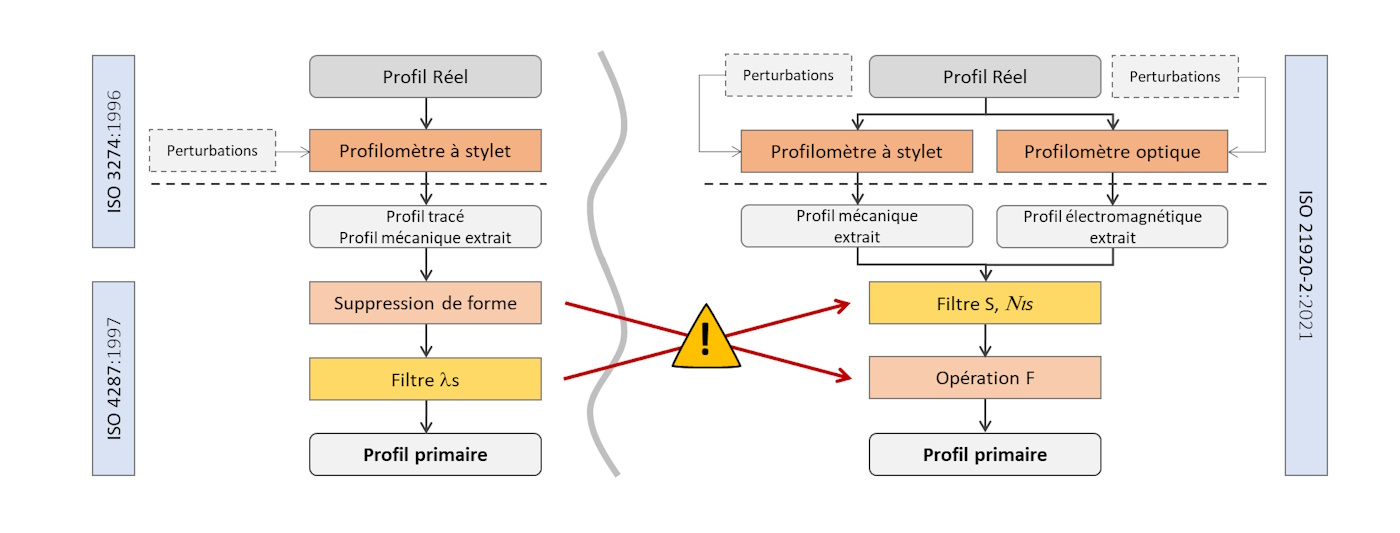
Avant 2021, la norme ISO 3274 définissait la chaîne de mesure selon le schéma ci-dessus à gauche. Le profil mesuré par un profilomètre est aujourd'hui forcément numérique ; il est appelé le profil extrait. Il est échantillonné en X et numérisé en Z et représente une abstraction de la surface réelle (plusieurs filtres interviennent dans le capteur du fait de la bande passante limitée de l'instrument). La surface réelle de l'échantillon mesuré peut être modélisée par une surface mécanique (enveloppe) lorsqu'elle est mesurée par un stylet à contact, ou par une surface électromagnétique, qui représente l'interface perçue par un capteur optique (dont la caractéristique n'est pas tout à fait la même selon la technique optique utilisée). Pour produire le profil primaire qui est le point de départ de l'analyse métrologique, on doit procéder au retrait de la forme et appliquer un filtre λs (Filtre S) qui supprime la microrugosité. Ces deux opérations ne sont pas appliquées dans le même ordre entre l'ancienne et la nouvelle norme. Et parfois, le filtre S est omis, comme avec la norme allemande VDA 2006 utilisée dans l'automobile.
Les paramètres sont ensuite calculés à partir du profil (ou de la surface) primaire, ou en appliquant un filtre S ou L. Le schéma suivant montre la différence de traitement entre les profils et les surfaces, et notamment le fait que la surface primaire contient la forme, contrairement au profil primaire, pour des raisons historiques.
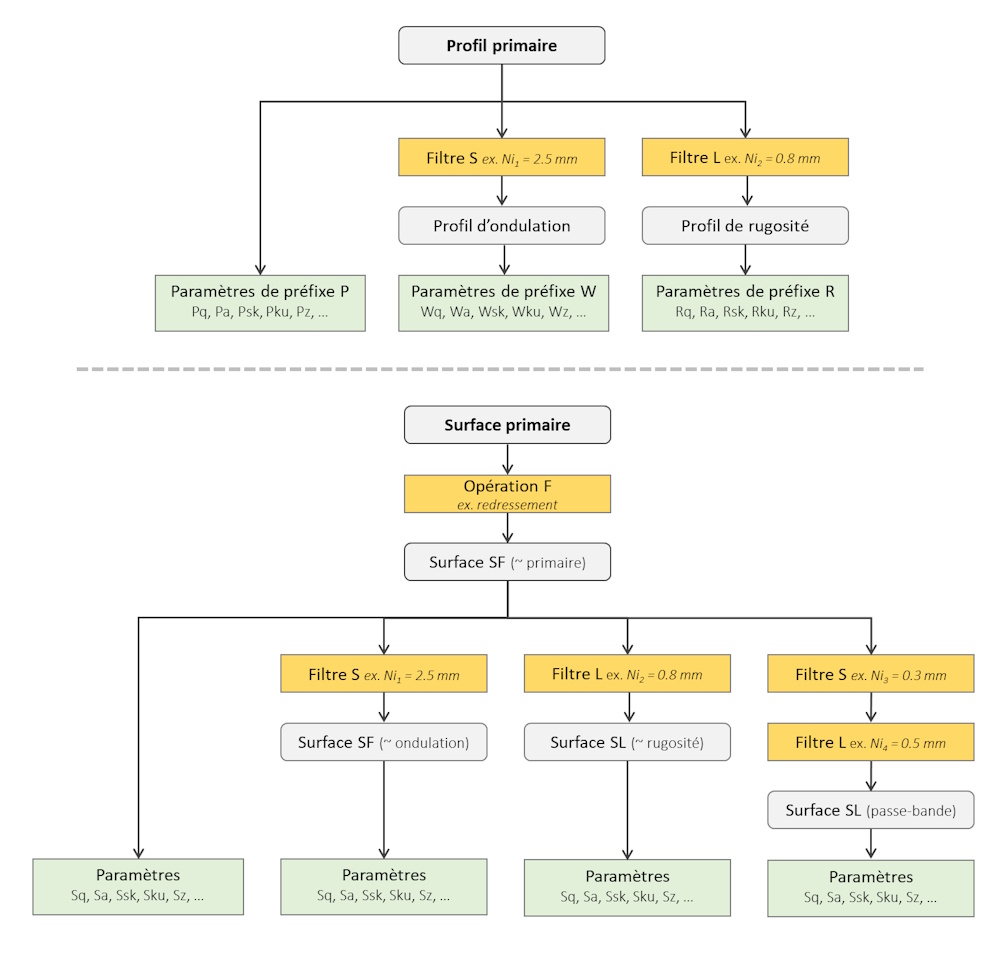
En réalité, le filtre L est obtenu par la soustraction du profil (ou de la surface) d'ondulation, du profil (ou de la surface) primaire. C'est pourquoi le même cut-off est utilisé dans les deux cas. Mais lors de l'analyse d'une pièce, il est tout à fait possible d'avoir la rugosité et l'ondulation calculées avec un cut-off différent, si c'est justifié d'un point de vue fontionnel. Les paramètres de profil sont calculés selon l'ISO 21920-2, et les paramètres surfaciques sont calculés selon l'ISO 25178-2.
2. Vocabulaire
Le nouveau vocabulaire introduit initialement pour les surfaces dans l'ISO 25178 a été ensuite décliné sur les profils dans l'ISO 21920 :
Filtre S : filtre qui atténue les courtes longueurs d'ondes (S pour short = court). C'est donc un filtre lissant, utilisé soit pour filtrer la microrugosité (avec un petit cut-off) soit pour créer l'ondulation (avec le cut-off principal).
Filtre L : filtre qui atténue les grandes longueurs d'ondes (L pour long). Ce filtre est obtenu par la différence entre le profil ou la surface primaire et le profil ou la surface d'ondulation (avec le cut-off principal).
Opération F : opération qui supprime la forme ou redresse le profil ou la surface. Voir les différentes méthodes pour les opérations F.
Surface SF : surface obtenue par l'application d'un filtre S et d'une opération F.
Surface SL : surface obtenue par l'application d'un filtre S et d'un filtre L.
Surface primaire : surface obtenue par l'application d'un filtre S.
Nesting index : ou indice d'imbrication (ou encore indice gigogne), est soit un cut-off, dans le cas d'un filtre linéaire, soit la taille de l'élément structurant, pour un filtre morphologique, ou encore la valeur de l'élagage de Wolf, dans le cas d'une segmentation. Le nesting index est simplement le terme générique du critère réglant la force du filtre.
Profil primaire : profil filtré avec un filtre S (λs) et dont la forme a été supprimée par un opérateur F. C'est l'équivalent d'un profil SF.
Profil d'ondulation : profil filtré avec un filtre S (λc) pour ne conserver que les grandes longueurs d'onde. C'est également l'équivalent d'un profil SF, avec un autre cut-off.
Profil de rugosité : profil filtré avec un filtre L (λc) pour ne conserver que les courtes longueurs d'onde. C'est également l'équivalent d'un profil SL (le filtre S provient du profil primaire).
3. Historique des filtres
Les premiers filtres ont été implémentés comme des filtres électroniques passe-haut en utilisant des résistances et des condensateurs soudées à l'arrière de commutateurs permettant de changer de cut-off. Le but initial de ces filtres étaient d'éviter les trop grandes variations du signal afin de tracer le profil sur une bande de papier carboné ou d'indiquer la rugosité sur un cadran galvanométrique. Ces filtres RC ont été utilisés pendant plus de trente ans sur tous les profilomètres à contact. Dans les années 1980, les permiers microordinateurs ont été connectés aux profilomètres par l'intermédiaires de cartes de conversion analogique-numérique. Les premiers logiciels d'analyse des profils ont implémenté les filtres RC sous forme numérique afin d'obtenir les mêmes effets sur les profils qu'avec les filtres analogiques.
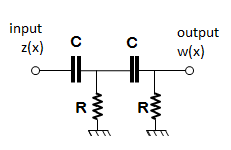

Filtre analogique RC2 (gauche) et sélection de cut-off sur un Talysurf 10 (droite)
L'inconvénient majeur du filtre RC est qu'il déphase le signal de façon non linéaire selon la longueur d'onde, produisant des effets indésirables sur le profil filtré autour des vallées et des pics importants.
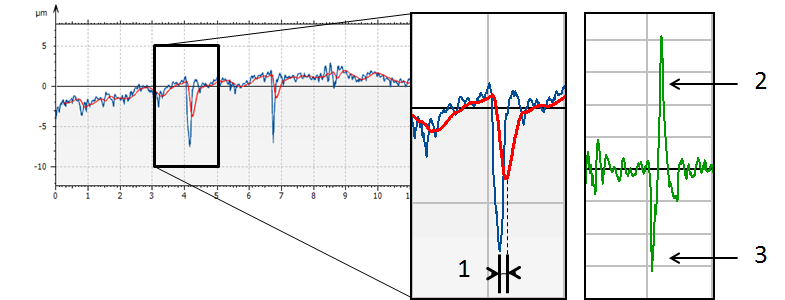
Décalage de phase des irrégularités avec un filtre RC2
Ci-dessus : zoom sur une vallée (1). La ligne moyenne est "en retard" sur le profil primaire. L'effet sur le profil de rugosité fait apparaître des pics suramplifiés autour de la vallée (2) et une minimisation de la profondeur de la vallée (3).
Au début des années 1990, une version à phase correcte du filtre RC2 a été créée dans une tentative de résoudre ce problème. Il s'est appelé RC2-PC (pour Phase Correct). Cependant, un travail plus rigoureux mené en parallèle a abouti à la création d'un nouveau filtre, naturellement à phase correcte, le filtre gaussien.
Introduction au filtrage
Cette video présente les bases du filtrage en états de surface et explique l'effet des filtres sur le contenu spectral des profils et surfaces. Durée : 19 min 40.
4. Le filtre gaussien
Le filtre gaussien a été introduit pour les profils dans la norme ISO 11562 en 1996. Cette norme définit la fonction de transfert du filtre passe-bas qui produit l'ondulation (ligne moyenne). En soustrayant l'ondulation au profil primaire, on obtient le profil de rugosité.
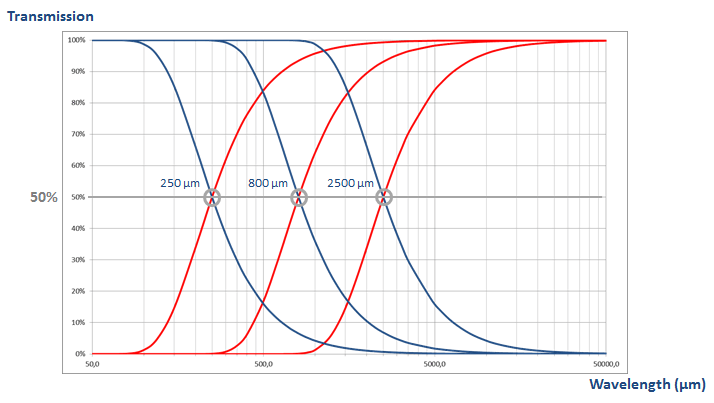
Fonction de transfert pour le filtre de rugosité (bleu) et d'ondulation (rouge) pour plusieurs valeurs de cut-off. Ces courbes se croisent à 50% de transmission.
Il est courant de couper une portion du profil filtré à chaque extrémité, d'une longueur qui dépend du fabricant d'instrument. Certains coupent l'équivalent d'un 1/2 cut-off de chaque côté, d'autre coupent un cut-off entier. En théorie, il faudrait couper au minimum 0,6 cut-off. La conséquence est que le profil filtré est plus court que le profil primaire, de l'équivalent de 1 ou 2 cut-offs.
Dans MountainsMap, l'utilisateur peut configurer la longueur de coupure pour chaque type de filtre en allant dans les préférences, et peut même conserver la longueur totale en activant l'option Gérer les effets de bord.
En 2011, la norme ISO 16610-21 a remplacé officiellement l'ancienne norme ISO 11562 pour la définition du filtre gaussien, pour les profils ouverts et fermés. Pour les surfaces, le filtre équivalent est défini dans l'ISO 16610-61.
Des détails complémentaires sur le filtrage des surfaces peuvent être trouvés dans [SEEWIG 2013]
Pour une longueur d'onde équivalente à la valeur du cut-off, le filtre atténue (ou transmet) 50% de l'amplitude de la longueur d'onde. Les filtres ne doivent pas être vus comme des interrupteurs qui bloquent ou laissent passer les longueurs d'onde. Leur fonction de transfert est continue et progressive. Par conséquent, le choix de la valeur du cut-off est critique selon l'application, afin de séparer correctement les longueurs d'onde (ou les échelles) qui appartiennent à l'ondulation et la rugosité.
Le filtre gaussien est utilisé avec succès depuis plus de vingt ans pour de très nombreuses applications. Néanmoins, ce filtre ne se comporte pas de façon correcte autour des ruptures telles que les points aberrants, les marches ou en présence de forme. C'est pourquoi les filtres robustes ont été développés.
5. Le filtre robuste gaussien
Un filtre robuste a une ligne moyenne (un plan moyen) qui suit correctement la tendance naturelle du profil (de la surface) sans être perturbé par les ruptures du profil. Le Filtre robuste de regression gaussien est décrit dans l'ISO 16610-31 comme un algorithme itératif qui calcule des coefficients de pondération en fonction de la distance entre la ligne moyenne est le profil primaire.

Le filtre gaussien classique (à gauche) est perturbé autour des discontinuités alors que le filtre gaussien robuste (à droite) ne l'est pas.
Le filtre gaussien robuste est à privilégier pour les surface structurées ou stratifiées, ou en présence de forme, de rainures ou de pores. En particulier, c'est une bonne alternative au filtre double-gaussien défini dans l'ISO 13565-1 (anciennement DIN 4777)
6. Cut-off et Nesting index
Le terme cut-off est utilisé aujourd'hui pour définir la longueur d'onde à laquelle le filtre atténue l'amplitude de 50%. Cela signifie aussi que cette longueur d'onde est transmise à 50%. Les utilisateurs doivent donc choisir la valeur du cut-off soigneusement afin de ne pas couper en plein milieu une population de longueur d'onde. Autrement dit, si la pièce mesurée contient de l'ondulation et de la rugosité, le spectre de longueurs d'onde montrera deux populations distinctes, l'une pour l'ondulation, l'autre pour la rugosité. Le cut-off devra séparer les deux populations afin de ne pas altérer l'une ou l'autre de ces populations. Et dans certains cas, la pièce mesurée est suffisamment plate pour qu'il n'y ait pas d'ondulation. Dans ce cas le filtre est superflu puisqu'on récupère directement la rugosité.
Pour les profils, les valeurs de cut-off sont choisies couramment dans une série géométrique spécifiée dans l'ISO 4288 : ... 0,08 mm; 0,25 mm; 0,8 mm; 2,5 mm ...
Cependant, pour certaines applications qui tombent en dehors du cadre habituel du système GPS (qui s'adresse principalement aux mécaniciens), l'utilisateur doit pouvoir choisir des valeurs différentes pour le cut-off. Dans ce cas, l'utilisateur devra lui-même étudier la corrélation fonctionnelle entre le choix du cut-off d'un côté et la performance de la fonction étudiée de l'autre. Par exemple, les profils mesurés sur des produits plats sidérurgiques peuvent être filtrés avec un cut-off de 5 mm pour isoler l'ondulation qui est imprimée sur la tôle par la vibration des rouleaux de laminoirs.
Pour les surfaces, la série recommandée est décrite dans l'ISO 25178-3 : ... 0,1 mm; 0,2 mm; 0,25 mm; 0,5 mm; 0,8 mm; 1,0 mm ...
Le terme nesting index (indice d'imbrication ou indice gigogne) a été forgé pour étendre le concept de cut-off qui ne s'applique que pour les filtres linéaires. Dans la série de normes ISO 16610, de nouveaux filtres non-linéaires sont définis, tels que le filtre morphologique ou le filtre spline robuste. Par conséquent, le terme cut-off ne peut être utilisé pour ces filtres et le terme nesting index est utilisé à la place. Le nesting index est un paramètre qui contrôle le filtre et la façon dont il agit sur les échelles ou les longueurs d'onde.
Pour un filtre Spline, le nesting index est simplement un cut-off. Pour un filtre morphologique, le nesting index est la forme de l'élément structurant (ex: une sphère) et sa taille (son diamètre).
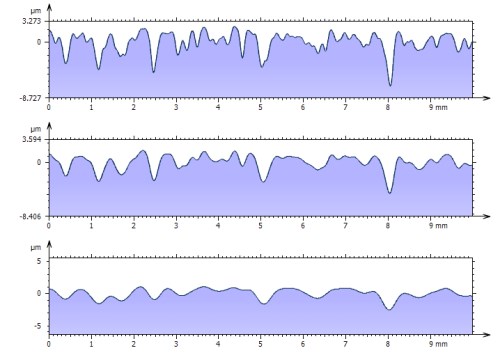
Profils filtrés (ondulation) avec différents cut-offs
(du haut en bas : 0,2 mm, 0,4 mm et 0,8 mm)
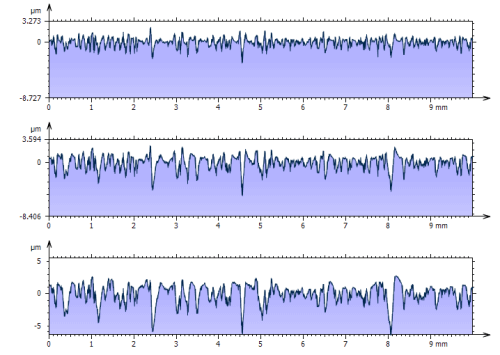
Profils filtrés (rugosité) avec les mêmes cut-offs.
7. Le filtre spline cubique
Une spline cubique est une courbe géométrque qui relie de façon souple une série de points. Les splines sont utilisées par exemple pour dessiner des formes courbes dans les logiciels de CAO et sont également utilisées pour interpoler entre des points d'une courbe.
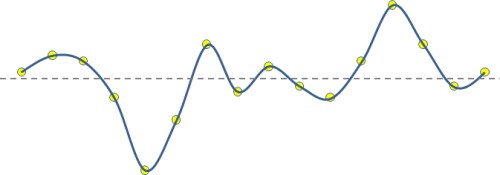
Points de données (en jaune) connectés par une courbe spline (en bleu).
Après l'application d'un filtre spline, la courbe spline ne passe plus par les points de données, mais par des points suspendus. Ces points supendus sont connectés aux points de données par un ressort fictif d'une raideur donnée, notée β, qui est appelée le paramètre de tension. En choisissant la valeur de ce paramètre de tension (entre 0 et 1) on peut contrôler le comportement du filtre.

Points suspendus (en vert) connectés aux points de données du signal originel par un ressort. La courbe spline (en bleu) représente maintenant le profil filtré (ondulation).
Par défaut (avec β = 0.6252) le comportement du filtre spline est très proche de celui du filtre gaussien.
Le filtre spline est décrit dans la norme ISO 16610-22 pour les profils et dans la norme ISO 16610-62 pour les surfaces.
En pratique, ce filtre spline n'apporte que très peu d'avantage par rapport au filtre gaussien et en possède les mêmes inconvénients.
8. Le filtre spline robuste
Une variante du filtre spline a été conçue afin de le rendre robuste envers les discontinuités. Le filtre spline robuste est défini dans la norme ISO 16610-32 pour les profils et dans la norme ISO 16610-62 pour les surfaces. De par sa nature non-linéaire, son implémentation est assez complexe et ce filtre est moins fréquemment disponible dans les logiciels d'analyse.
Bien que ce filtre spline robuste soit en théorie meilleur que le filtre gaussien robuste, les résultats étant très proches dans les deux cas, c'est le filtre gaussien robuste qui est préféré en pratique .
9. Les filtres par ondelettes
Les filtres par ondelettes sont basés sur une analyse harmonique localisée spatialement réalisée grâce à des signaux à support court-terme appelés ondelettes mères. Pour les états de surface, les filtres par ondelettes sont utilisés pour décomposer les niveaux d'échelle des profils et des surfaces. Cette analyse multi-échelle permet d'identifier les niveaux d'échelle particuliers où se manifestent certains phénomènes, et également de retirer un phénomène spécifique en altérant un niveau d'échelle particulier, et en reconstruisant le signal sans ce phénomène (discontinuité ou structure).
Les filtres par ondelettes sont définis dans la norme ISO 16610-29 pour les profils et dans la norme ISO 16610-69 pour les surfaces. Pour le moment seules les ondelettes splines sont définies dans cette norme. Les ondelettes complexes seront ajoutées à l'avenir, spécialement pour les surfaces. La littérature technique décrit de nombreuses autres ondelettes mères (Coiflet, Daubechies, ...) qui sont utiles chacunes dans des applications spécifiques comme l'analyse d'images infrarouges ou de signaux sismiques mais qui sont moins utiles pour les états de surface.
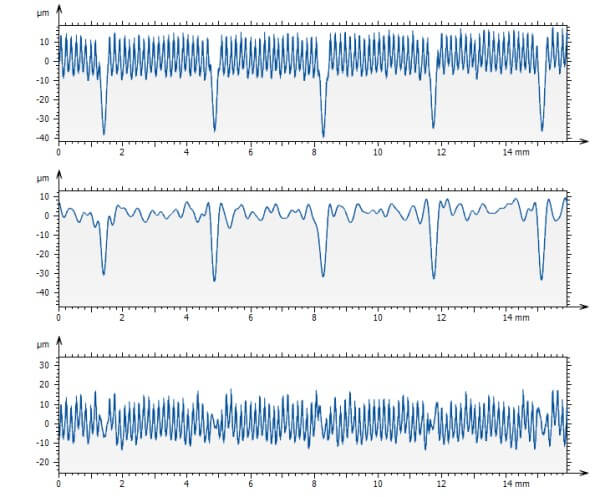
Ci-dessus : un profil contenant deux signaux périodiques superposés est décomposé par un filtre par ondelettes discret avec une ondelette de Meyer. Les deux signaux sont parfaitement séparés.
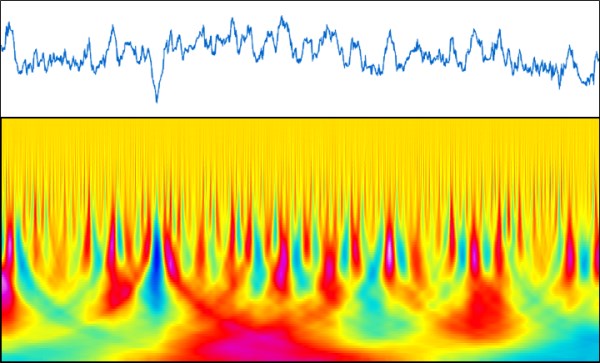
Exemple d'une Transformée en ondelettes continue sur un profil. Les échelles courtes sont au-dessus et les échelles longues en bas. L'image montre les différentes structures caractéristiques à chaque échelle.
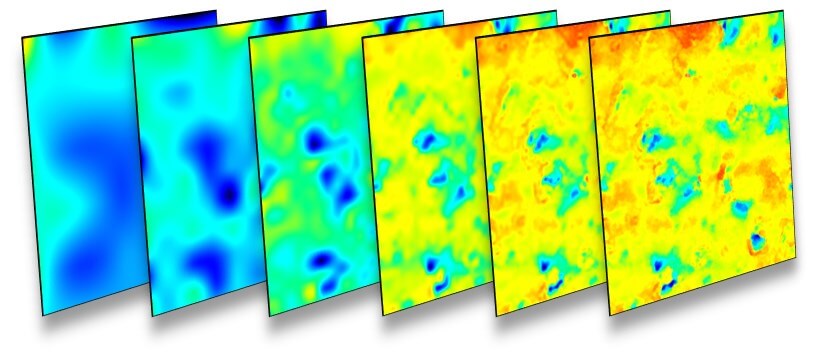
Ci-dessus : une surface est décomposée par un filtre par ondelettes splines discret. Chaque image est reconstruite en ne conservant que les niveaux d'échelle au-dessus d'un seuil, de 2 niveaux (à gauche) jusqu'à 7 niveaux (à droite). Les échelles larges sont à gauche. L'image toute à droite contient tous les niveaux d'échelle.
Ces fonctions sont disponiles dans le module Fourier & Wavelets Analysis module pour les produits MountainsMap® traitant les surfaces, et dans le module Advanced Profile pour les produits MountainsMap® traitant les profils.
10. Effets de bords
Les filtres peuvent être implémentés soit par convolution soit par Transformée de Fourier (le plus souvent la FFT). Dans le premier cas, la matrice de filtrage ne peut filtrer jusqu'aux bords et une bande de largeur égale à la moitié de la taille de la matrice reste non filtrée. Dans le deuxième cas, des phénomènes de recouvrement de spectre lors de la Transformée de Fourier entraînent une perturbation des bords du signal filtre. C'est pour cela qui est conventionnel de couper une portion du profil filtré (ou de la surface filtrée). Mais aucune norme ne spécifie clairement de combien il faut couper de sorte qu'en pratique certains logiciels coupent d'un 1/2 cut-off et d'autre d'un cut-off. Dans MountainsMap, cette valeur est configurable dans les Préférences pour chaque type de filtre.
La norme ISO 16610-28 décrit plusieurs stratégie permettant de gérer les effets de bords afin que le signal filtré conserve la taille originelle. Certaines méthodes demandent une modification de l'équation du filtre au fur et à mesure qu'il s'approche des bords. D'autres méthodes étendent artificiellement la donnée originelle avant le filtrage de sorte qu'en coupant la donnée filtrée on retombe sur la taille initiale.
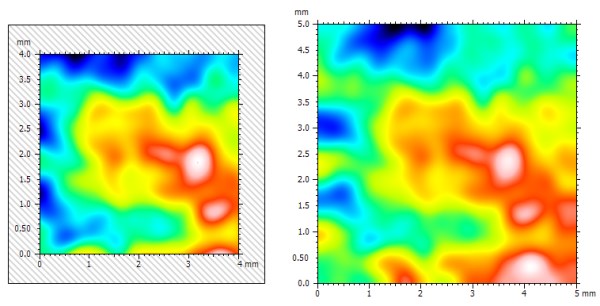
Ci-dessus : une surface de 5 mm x 5 mm filtrée par un filtre de 1 mm de cut-off. A gauche : 36% de l'aire est coupée. A droite : toute l'aire initiale est conservée.
11. Les filtres morphologiques
Un filtre morphologique est basé sur deux opérations morphologiques de base, la dilatation et l'érosion, qui fonctionne à l'aide d'un élément structurant d'une taille donnée. Par exemple, le profil ci-dessous est dilaté par un disque de rayon connu.

Le disque roule par dessus la surface et la trajectoire de son centre est enregistrée (ligne rouge). La dilatation tend à élargir les pics et combler les creux. L'élément structurant peut être, en théorie, de n'importe quelle forme. Si le disque roule sous la surface, on obtient une érosion.
Quand une dilataion est suivie d'une érosion, on obtient une fermeture morphologique qui est un filtre morphologique qui crée une enveloppe supérieure. Le disque roule sous la ligne de dilatation. L'enveloppe ferme les creux tout en suivant les aspérités saillantes de la surface (pics et collines).

Si la séquence est inversée, c'est-à-dire, une érosion suivie d'une dilatation, le filtre est appelé une ouverture morphologique et il crée l'enveloppe inférieure.
Les filtres morphologiques sont définis dans la norme ISO 16610-41 pour les profils et dans la norme ISO 16610-81 pour les surfaces.
Une application des filtres morphologiques est leur capacité à applatir une surface sur son enveloppe. L'exemple suivant montre une surface (à gauche) avec des particules qui ne sont pas posées sur une base plate, rendant difficile l'aplication d'un seuillage. Lorsque l'enveloppe inférieure est calculée puis soustraite à la surface initiale, on ramène son socle proche du plan, alignant de ce fait les particules sur une référence plane.
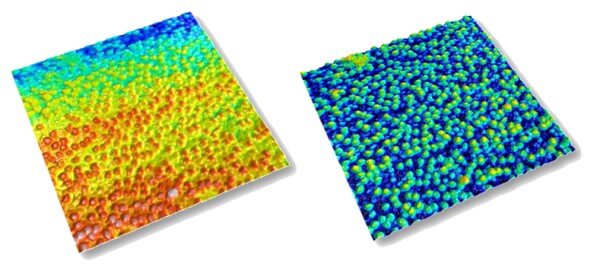
Si la surface avait été redressée à l'aide de l'enveloppe supérieure, toutes les particules auraient eu leur sommet aligné à la même hauteur.
Les filtres morphologiques peuvent également être cascadés pour créer une banque de filtres réalisant une analyse multi-échelle. Cette application est décrite dans la norme ISO 16610-49 pour les profils et dans la norme ISO 16610-89 pour les surfaces.
Les filtres morphologiques sont proposés comme opérateur dans le module : Advanced Topography et sont inclus dans MountainsMap® SEM et MountainsMap® Premium.
12. Filtres de suppression de points aberrants
Les profilomètres optiques, qu'ils soient confocaux, interférometrique ou à variation de focale, sont de plus en plus populaires. Ils sont précis, rapides et fournissent parfois une image couleur en plus de la topographie. Cependant ils ont un inconvénient : ils génèrent des points aberrants (pics extrêmes) qui ne sont pas réellement sur la surface.

Ces dispositifs optiques demandent à ce que la lumière soit réfléchie sur la surface et renvoyée vers un détecteur. Le schéma ci-dessus montre sur l'axe horizontal la force du signal optique reçu sur le détecteur. Lorsque le signal est suffisamment fort (à droite), le logiciel d'acquisition peut calculer la hauteur correctement et précisément. De l'autre côté, à gauche, si aucun signal ne revient sur le détecteur, il est impossible de fournir une hauteur et le logiciel génère un point non-mesuré (ou point manquant). C'est le cas si l'échantillon est trop sombre ou si le signal est réfléchi en dehors de l'objectif. Le problème intervient entre les deux cas, lorsqu'un signal parvient sur le détecteur mais que sa puissance n'est pas suffisante pour effectuer un calcul fiable (faible rapport signal-sur-bruit), entraînant la génération d'un point incorrect d'altitude fortement supérieure ou inférieure à la surface environnante. Ces points sont appelés des points aberrants (outliers).
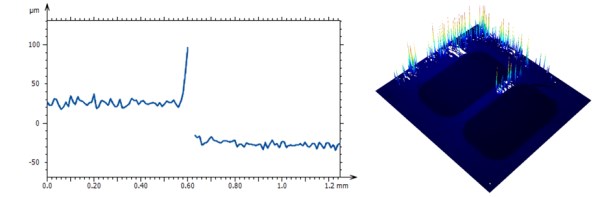
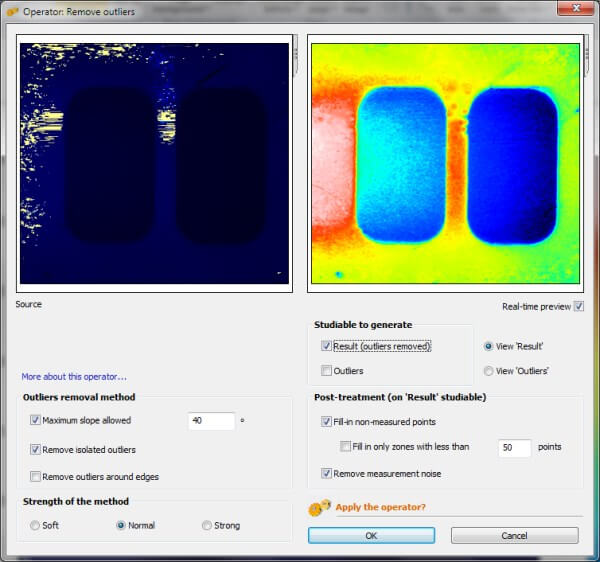
MountainsMap propose des outils dédiés qui détectent automatiquement ces points aberrants, les suppriment et interpole la zone supprimée.
L'outil propose une combinaison de filtres, chacun conçu pour une typologie particulière : points aberrants isolés ou sous forme de bandes autour des arêtes. Il est également possible de régler la pente locale maximale. Les points non-mesurés sont interpolés à l'aide d'une forme molle et un filtre lisseur peut être appliqué en final afin de produire des images propres pour l'affichage.
Cet outil est inclus dans MountainsMap® Imaging Topography et MountainsMap® Premium, ainsi que dans le module Advanced Topography
13. Filtres FFT
Des filtres avancés peuvent être utilisés afin d'éditer directement le spectre de Fourier d'une surface, qui est obtenu par Transformée de Fourier. Un filtre linéaire traditionnel est souvent implémenté en utilisant la FFT, en multipliant le spectre de Fourier avec la fonction de pondération du filtre, puis à calculer la Transformée de Fourier inverse. Le spectre de Fourier peut également être modifié manuellement ou en appliquant un seuillage, afin d'éliminer spécifiquement certaines longueurs d'onde ou certaines directionnalités.
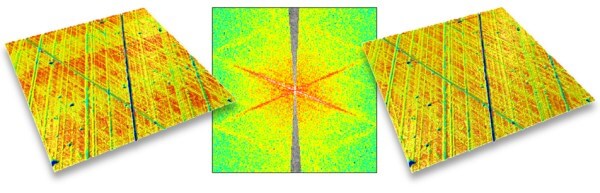
Ci-dessus, une surface mesurée par un profilomètre 3D montre un défaut de planéité lié à la rectitude de la table Y. Ce problème peut être corrigé en éliminant la directionnalité correspondante au défaut sur le spectre (au centre) et en reconstruisant la surface sans cette bande (à droite).

Le second exemple montre qu'il est même possible de retirer les stries dans une seule direction afin d'analuser l'autre direction séparément.
Les Filtres FFT sont inclus dans le module Fourier & Wavelets Analysis et dans MountainsMap® Premium.
14. Structure de la norme NF EN ISO 16610
La NF EN ISO 16610 est la norme de référence pour les filtres de profils et de surfaces, pour les états de surface et les écarts de forme. Le premier groupe de documents couvre les profils, le second groupe couvre les surfaces.
Concepts généraux
Filtres de profils
Filtres surfaciques
WD: Working Draft, DIS: Draft International Standard, FDIS: Final Draft International Standard, TS: Technical Specification, TR : Technical report.
Apprenez facilement la métrologie des surfaces grâce à nos cours en français et en vidéo disponibles sur notre chaîne Youtube :
Cours en vidéo de métrologie des états de surface.
