Paramètres surfaciques de champ
Les paramètres de champ (field parameters) sont ceux qui utilisent l'ensemble des points de la surface, par opposition aux paramètres de motifs (feature parameters). Ils se décomposent en trois familles : les paramètres d'amplitude, les paramètres spatiaux et les paramètres hybrides. Ils sont définis dans l'ISO 25178.
1. La période pré-normative
Les premiers fabricants d'instruments surfaciques de mesure d'état de surface ont d'abord proposé, dans les années 1990, des méthodes d'analyse issues de l'extrapolation de méthodes profilométriques. En l'absence de documentation officielle, les fabricants ont alors improvisé leur propre solution avec plus ou moins de bonheur, avec des paramètres surfaciques parfois calculés comme de simples moyennes de paramètres de profils calculés sur chaque ligne de la surface, ou calculés sur des profils radiaux autour du centre de la surface. Les conventions de nommage variaient d'un fabricant à l'autre, souvent à partir des noms des paramètres de profils (sRa, sWa...) et les algorithmes de calcul diffèraient d'un instrument à l'autre. Néanmoins, petit à petit les bonnes pratiques se sont diffusées, notamment grâce aux publications du Prof. Stout et de ses collaborateurs à Birmingham [STOUT 1993], et grâce aussi à la sortie du logiciel DigiSurface sur Macintosh en 1993, développé par Digital Surf et adopté par la suite par Taylor Hobson pour le Form Talysurf sous le nom Talymap.
Par la suite, la sortie du logiciel MountainsMap® en 1996 et la publication du rapport SurfStand [BLUNT 2003], ont contribué à l'uniformisation des méthodes d'évaluation des paramètres surfaciques. La version 5.0 de MountainsMap® a été le premier logiciel commercial à proposer en 2007 l'ensemble complet des paramètres surfaciques de champ issus des documents préliminaires de l'ISO 25178.

Des détails sur les paramètres surfaciques de champ de l'ISO 25178
peuvent être trouvés dans [BLATEYRON 2013a] (chapitre 2 de [LEACH 2013]).
2. Conventions de nommage
Dans la norme ISO 25178, tous les paramètres surfaciques commencent par la lettre capitale S ou la lettre capitale V. Contrairement aux paramètres de profils, il n'y a pas de préfixe reflétant la nature de la surface filtrée permettant de savoir si on a affaire à un paramètre de rugosité, d'ondulation ou de profil primaire. Sur un profil, on a Pa, Ra et Wa, mais sur une surface on a seulement Sa, qui peut donc être tantôt un paramètre de rugosité ou d'ondulation, selon les opérations de filtrage appliquées en amont. Ce choix s'explique par la multiplicité des méthodes de filtrage à la disposition des métrologues, définies dans [ISO 16610]. Ces filtres ne servent pas toujours à séparer l'ondulation de la rugosité mais altèrent parfois la surface de façon plus subtile.
3. Les paramètres d'amplitude
La plupart des paramètres de profils de l'ISO 4287 peuvent facilement être étendus pour le cas surfacique. Par exemple, Sq est simplement l'extension à un plan de l'équation du Rq qui est défini sur une ligne :
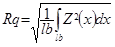
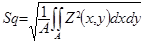
Sa, Sq, Ssk, Sku, Sp, Sv, etc. se définissent donc de la même façon par simple extrapolation au plan.
Les équations des paramètres font apparaître des intégrales plutôt que des sommes car les définitions sont données pour le cas continu. Bien-sûr, les implémentations sont toutes réalisées pour le cas discret et plusieurs approximations sont possibles pour les intégrales. Aucune méthode n'est privilégiée mais chaque méthode est affectée d'une incertitude plus ou moins importante.
Outre les paramètres extrapolés du profilométrique au surfacique, certains paramètres posent un peu plus de problèmes. Rz est défini dans l'ISO 4287 comme la hauteur maximale du profil sur une longueur de base et est moyennée sur l'ensemble des longueurs de base utilisées. En général, Rz est inférieur à Rt. Ce paramètre a connu de nombreuses définitions contradictoires, la première provenant de l'ISO 4287 (1984) et définie comme la hauteur des dix points. La définition a été modifiée fortement en 1997 et ce paramètre reste confus dans l'esprit des utilisateurs notamment du fait de sa similarité avec les paramètres Ry et Rmax.
Il faut noter que le paramètre Sz défini dans l'ISO 25178 est simplement la hauteur maximale de la surface, du point le plus bas au point le plus haut, comme le paramètre St était autrefois défini. St a d'ailleurs disparu de la norme ! Cette absence risque de créer à nouveau de la confusion à certains utilisateurs...
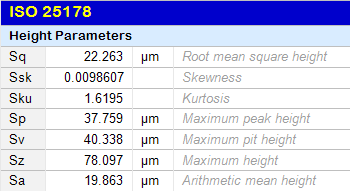
Paramètres surfaciques de hauteur
Description des paramètres d'état de surface surfaciques de l'ISO 25178-2. La première partie décrit en particulier les paramètres de hauteur et les paramètres liés à la courbe d'Abbott. Durée : 21 min 13
4. Les paramètres spatiaux
Une surface est dite isotrope quand elle présente les mêmes caractéristiques quelque soit la direction de mesure. C'est le cas, par exemple, des surfaces présentant un état de surface stochastique (aléatoire), c'est-à-dire qui n'ont pas de texture marquée. Ce type de surface est de plus en plus rare et la plupart des surfaces utilisées dans l'industrie présentent une orientation privilégiée (surfaces tournées, rectifiées, brossées) ou des structures périodiques (surfaces EBT, grainées, microbillées), notamment pour les procédés modernes de fabrication. Dans ces cas, on parle de surfaces anisotropes.
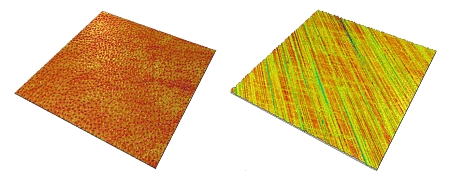
Surface isotrope (gauche) - surface anisotrope (droite)
L'isotropie d'une surface peut être évaluée à partir d'outils basés sur la Transformée de Fourier et l'autocorrélation.
L'autocorrélation est une fonction décrite par l'équation suivante :
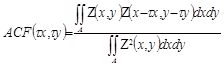
Cette fonction permet de générer une image qui peut être ensuite quantifiée.
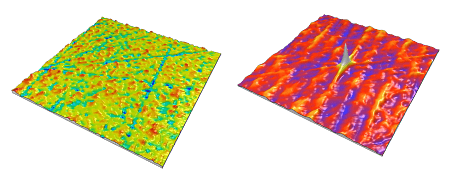
surface originelle (gauche) - autocorrélation (droite)
L'image d'autocorrélation présente toujours un pic central dont la hauteur est normalisée à 1,0. Dans certains cas, l'image montre des pics secondaires qui indiquent une corrélation de la surface avec elle-même à une autre position. C'est le cas pour les surfaces périodiques ou pseudo-périodiques. Par ailleurs, la forme du pic central est une indication de l'isotropie de la surface.
La forme du pic central peut être caractérisée en seuillant l'autocorrélation à un seuil s de 0,2 puis en mesurant les longueurs minimale et maximale du lobe dépassant le seuil.
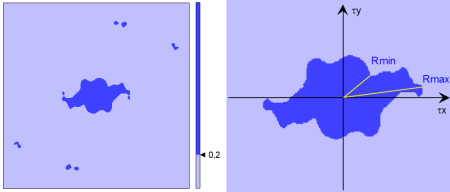
Rmin et Rmax sont les rayons minimum et maximum calculés sur le lobe central, du centre à son périmètre. Les rayons sont calculés à partir des points du périmètre, de coordonnée (tx,ty). Le seuil de 0,2 est une valeur par défaut pouvant être adaptée selon les applications, notamment afin d'assurer que le lobe central ne touche pas les bords de l'image.
Il est ainsi possible de définir un paramètre qui sera un indicateur d'isotropie de la surface :
Str, rapport d'aspect de la texture
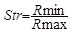
Les rayons minimum et maximum sont mesurés sur le lobe central, lui-même issu du seuillage du pic central d'autocorrélation. Si la surface présente les mêmes caractéristiques dans toutes les directions, le lobe central sera quasiment circulaire et les valeurs min et max très proches l'une de l'autre. Si la surface présente une direction de texture privilégiée, le lobe central sera très alongé et le rayon max sera très supérieur au rayon min.
Le paramètre Str prend une valeur entre 0 et 1, et est sans unité. Il peut être exprimé en poucentage entre 0% et 100%. Une surface isotrope a une valeur de Str proche de 1 (100%) alors qu'une surface fortement anisotrope aura une valeur de Str proche de 0.
La valeur Rmin fournit également une indication sur le contenu spectral de la surface. Une surface contenant essentiellement que de grandes longueurs d'onde aura une valeur élevé de Rmin, et inversement. Ceci conduit à la définition du paramètre Sal :
Sal, longueur de décroissance de l'autocorrélation Sal = Rmin
Le paramètre est exprimé en unité de longueur (µm ou mm).
Un autre outil intéressant est le spectre polaire. Le spectre de Fourier, quand il est intégré en coordonnées polaires, permet de déterminer les directions privilégiées de la texture. L'angle qui correspond au spectre le plus puissant correspond à la direction de texture principale.
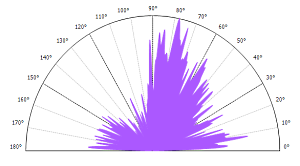
La visualisation du spectre polaire montre clairement les directions principales. La direction principale du spectre donne le paramètre Std :
Std, Directionnalité de texture
Cet angle est exprimé en degrés, dans le sens trigonométrique, depuis l'axe X.
5. Les paramètres hybrides
Les paramètres hybrides utilisent à la fois les informations de hauteur et les informations latérales. Ils sont en général parmi les paramètres les plus pertinents dans beaucoup d'applications (plus que la simple évaluation de la hauteur, comme le Sa).
Sdq, Pente moyenne quadratique
Ce paramètre calcule la pente locale sur chaque triangle de la surface, et effectue le même calcul que pour le Sq mais en remplaçant les hauteurs Z(x,y) par les pentes calculées. Le paramètre est exprimé en µm/mm ou en µm/µm ou même sans unité. Il est également possible de convertir la pente en un angle en utilisant l'arctangente. Ce paramètre caractérise la complexité de la surface. Plus le relief évolue vite (forte variation en Z dans un intervalle latéral court), plus la surface est complexe. A l'inverse, une surface très lisse et peu haute offrira un Sdq très faible.
Un autre paramètre utile pour caractériser la complexité de la surface est le Sdr.
Sdr, Surface développée
Ce paramètre calcule l'aire de chaque triangle élémentaire de la surface et les somme pour obtenir l'aire curviligne qui suit chaque aspérité et élément du relief de la surface. Cette aire est divisée par l'aire horizontale du support, afin de caractériser comment la surface diffère d'un plan horizontal. Comme les valeurs en pratique sont très proche de 1,000, le calcul ne donne que l'excès de l'aire par rapport à 1,0. Un Sdr de 3,5% correspondra à une aire développée 1,035 fois plus grande que l'aire projetée.
Le Sdr est exprimé en %. Plus la valeur est grande, plus la surface présente des complexités. Une valeur très proche de 0% indique une surface plate et lisse.
Ce calcul a un lien avec l'analyse fractale et le Sdr correspond en principe à la valeur de "area-scale" pour l'échelle la plus petite.
Les paramètres de base (amplitude) sont inclus dans tous les produits Mountains®. Les paramètres spatiaux et hybrides et les paramètres fonctionnels sont proposés dans le module optionnel : Advanced Topography et sont inclus dans MountainsMap® Premium.
Apprenez facilement la métrologie des surfaces grâce à nos cours en français et en vidéo disponibles sur notre chaîne Youtube :
Cours en vidéo de métrologie des états de surface.