Comment sont validés les algorithmes de paramètres ?

1. Vers une référence indépendante

Il y a un besoin fort d'avoir une référence indépendante, qui n'impose pas trop de contraintes à l'écriture des algorithmes de calcul, mais permette aux développeurs de vérifier la précision de leurs implémentations. Les développeurs doivent rester libres de leurs implémentations et de leurs optimisations ou des approximations assumées si le programme tourne sur un matériel léger et peu puissant.

Une telle référence indépendante ne peut être fournie que par la Nature et plus précisément, par les mathématiques. La plupart des paramètres sont maintenant définis dans le cas continu par des équations mathématiques. En définissant une surface ou un profil (un étudiable) également via une équation, il est alors possible de la combiner avec l'équation du paramètre et de calculer un résultat sous la forme d'une expression formelle, toujours mathématique. Ensuite, il suffit de calculer une valeur numérique à la précision souhaitée, en assignant une valeur aux termes de l'équation, comme l'amplitude, la période, etc. Par exemple, sur un simple profil sinusoïdal défini par :

z(x) = A sin (x)

avec A la demi-amplitude et x défini dans l'intervalle [0; 2nπ]. On peut choisir la longueur L pour qu'elle soit un multiple de la période, dans la même unité (par exemple, µm). The paramètre peut donc être calculé en substituant dans son équation l'équation du profil :

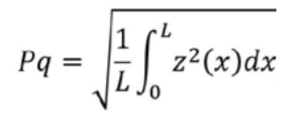
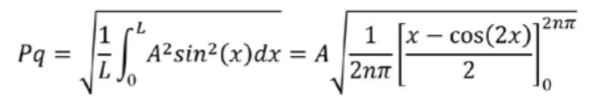
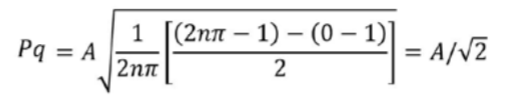
Afin de tester l'algorithme de calcul séparément, il est testé sans filtrage, sans redressement ni aucune autre opération. Les filtres et suppressions de forme sont testés séparément et le processus global est pris comme une succession de boîtes noires, chacune testée de façon unitaire à l'aide d'une référence mathématique.

Dans notre exemple, nous avons donc Pq = Pt /(2√2) pour un profil sinusoïdal (A = Pt/2) et l'on voit que c'est indépendant de la période. Par exemple, pour une amplitude de Pt = 1µm, on doit obtenir Pq ≈ 0,353553 µm et ce résultat peut être calculé avec autant de décimales que nécessaire.

La précision d'un paramètre calculé dans un logiciel dépend, bien-sûr, de l'algorithme, mais aussi du nombre de points en X et de la profondeur de numérisation en Z du profil discret utilisé dans la vérification. Donc, les profils générés pour la vérification pratique doivent introduire le moins possible d'imprécisions et permettre de vérifier uniquement les contributions de l'algorithme lui-même.

2. Généralisation des références mathématiques

Depuis plusieurs années, Digital Surf investit dans la recherche sur de nouvelles méthodes pour valider les paramètres et les filtres du logiciel Mountains®. Une collaboration avec l'Université de Nottingham et le NPL (National Physical Laboratory) en Angleterre, nous a permis de développer des paires de référence pour la plupart des normes définissant des paramètres. Une paire de référence est constituée 1) d'une définition mathématique d'un étudiable, et 2) d'une expression formelle du résultat d'un paramètre lorsque calculé avec cet étudiable.

Ce travail mathématique intensif a permis à Digital Surf de valider les paramètres de la norme ISO 25178 et plus récemment les paramètres de profil de la norme ISO 21920 (et par extension ceux des normes ISO 4287 et ISO 13565), ainsi que le filtre gaussien. Grâce à ce travail, Digital Surf a amélioré les algorithmes du logiciel Mountains® et a identifié quels paramètres sont sensibles à quelle caractéristique.

3. Vérification des paramètres surfaciques

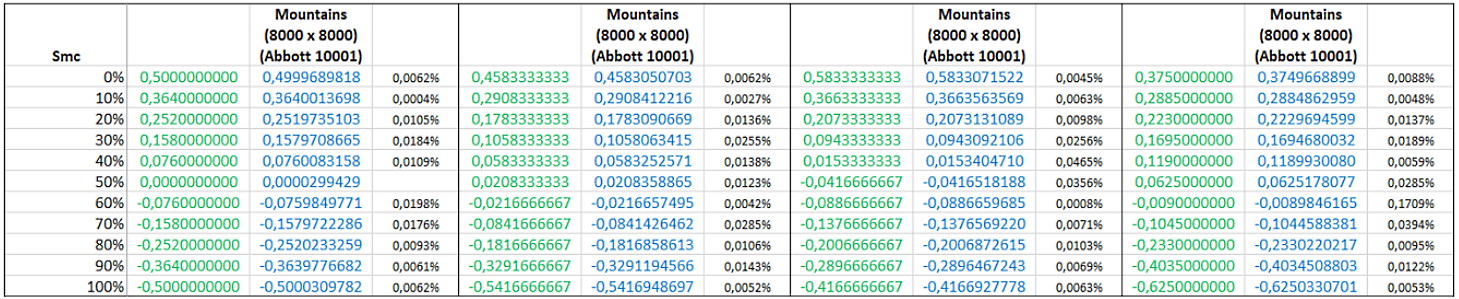
Un certain nombre de surfaces ont été définies mathématiquement, depuis une simple combinaison de sinusoïdales en X et Y, jusqu'à des polynômes de Bernouilli ou de Chebychev à différents degrés, et les équations ont été injectées dans chaque équation de paramètre pour obtenir une expression formelle du résultat. Ensuite une approximation numérique a été calculée sur 13 décimales en assignant une valeur aux termes de l'équation pour avoir une valeur à laquelle comparer les résultats calculés par Mountains®. Puis les surfaces ont été synthétisées sous forme discrète en haute résolution pour effectuer les calculs dans Mountains® v8 et calculer les écarts avec la valeur de référence. Le tableau ci-dessous donne les résultats pour la surface 4-term cosine. Les écarts sont en général inférieurs à ±0,001 %, ce qui est plus que suffisant pour la plupart des applications.

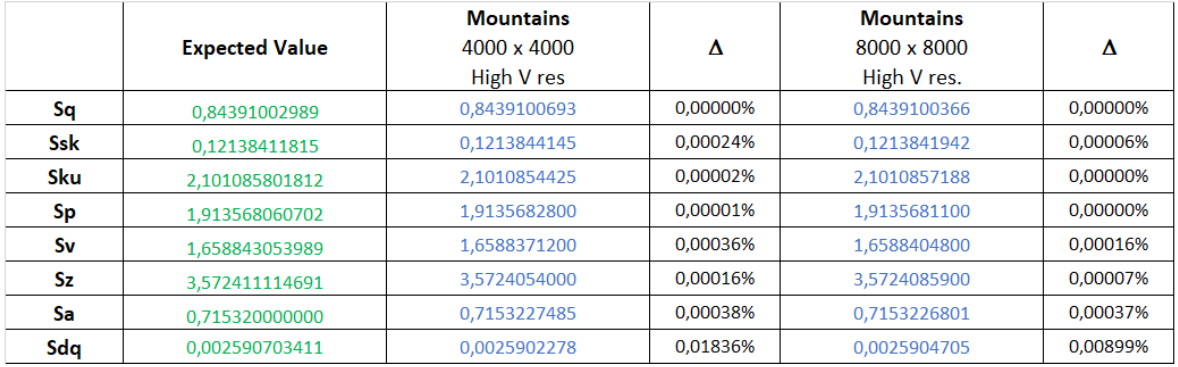
Il n'est pas toujours possible d'obtenir une expression formelle pour tous les paramètres et avec toutes les équations de surfaces, car certaines résolutions formelles sont trop complexes. Mais au final, il a été possible de valider l'ensemble des paramètres de champ, y compris Sdq (gradient), Sdr (aire développée), les paramètres de taux de portance (Smc, Smr) et leurs dérivées, Sk, Spk, Svk etc. ainsi que les paramètres de volume Vmp, Vmc, Vvc, Vvv.

Des résultats ont été obtenus sur plusieurs formes de courbes d'Abbott utilisables pour les paramètres fonctionnels. Une douzaine de formes ont été générées à l'aide d'un polynôme et les taux de portance ont été calculés pour différents points de la courbe. Dans la plupart des cas, les écarts sont inférieurs à 0,1 % et souvent beaucoup moins.

(Cliquer sur les tables pour les voir en grand )

Les paramètres les plus difficile à vérifier ont été ceux basés sur l'autocorrélation (Sal, Str) où il a été nécessaire de créer des équations dans le domaine de l'autocorrélation au lieu du domaine spatial. Cela a nécessité une procédure particulière pour implanter les tests directement dans le code source de Mountains® pour valider le seuil à s = 0,2 et la précision de la détection des rayons minimum et maximum sur le lobe d'autocorrélation. En faisant varier l'équation, il a été possible de générer des lobes oblongs ou compacts, fins ou larges et de tester la robustesse de l'algorithme.

Pour le moment, il manque des paires de référence pour les paramètres de motifs (Feature parameters) qui sont des algorithmes topologiques plutôt que des équations linéaires. La seule solution pour les vérifier consiste à faire des revues de code pour s'assurer que les algorithmes sont correctement implémentés. Mais des références mathématiques seront nécessaires à terme aussi pour ces paramètres.