Surface stochastique ou déterministe ?


Stochastique et déterministe sont deux termes que l'on rencontre de plus en plus souvent pour qualifier les surfaces modernes. Quelle est la signification de ces termes ? Comment se comparent-ils avec les concepts habituels de rugosité et d'ondulation ? Quelle implication sur la fonction de la surface ?


1. Classifier les surfaces

Les métrologues ont l'habitude de classifier les surfaces d'après leur rugosité, sur un axe allant de rugueux à lisse. Une surface est dite rugueuse quand sa longueur d'onde moyenne, c'est-à-dire la distance latérale entre deux passages à zéro sur le profil, est petit. Intuitivement, un profil avec de nombreuses variations de hauteur par millimètre en X est considéré comme plus rugueux qu'un profil avec moins de variations. Bien-sûr, l'amplitude du profil est aussi importante.

Il est plus difficile de comprendre l'influence des motifs ou des structures d'un profil. Les motifs se répètent plus ou moins à l'identique sur un profil ou une surface. Ils peuvent être géométriques, comme des piliers cylindriques dressés sur une surface plane, ou peuvent être plus irréguliers, comme les bosses d'un plastique grainé.

La majorité des paramètres classiques, comme Rq (ou Sq), appelés paramètres de champ, caractérisent seulement les hauteurs ou l'amplitude du profil (ou de la surface). Ils utilisent tous les points mesurés pour calculer les paramètres. Même quand ils sont associés à un filtre L, ils discriminent assez mal l'influence de la forme des motifs sur la fonction. La figure 1 montre trois profils qui ont la même valeur de Rq bien qu'ils aient, de façon évident, des fonctions différentes. Le premier profil est parfaitement périodique (sinusoïdal), le deuxième comporte des rainures périodiques rectangulaires et le troisième est un peu plus irrégulier bien qu'il soit pseudo-périodique.


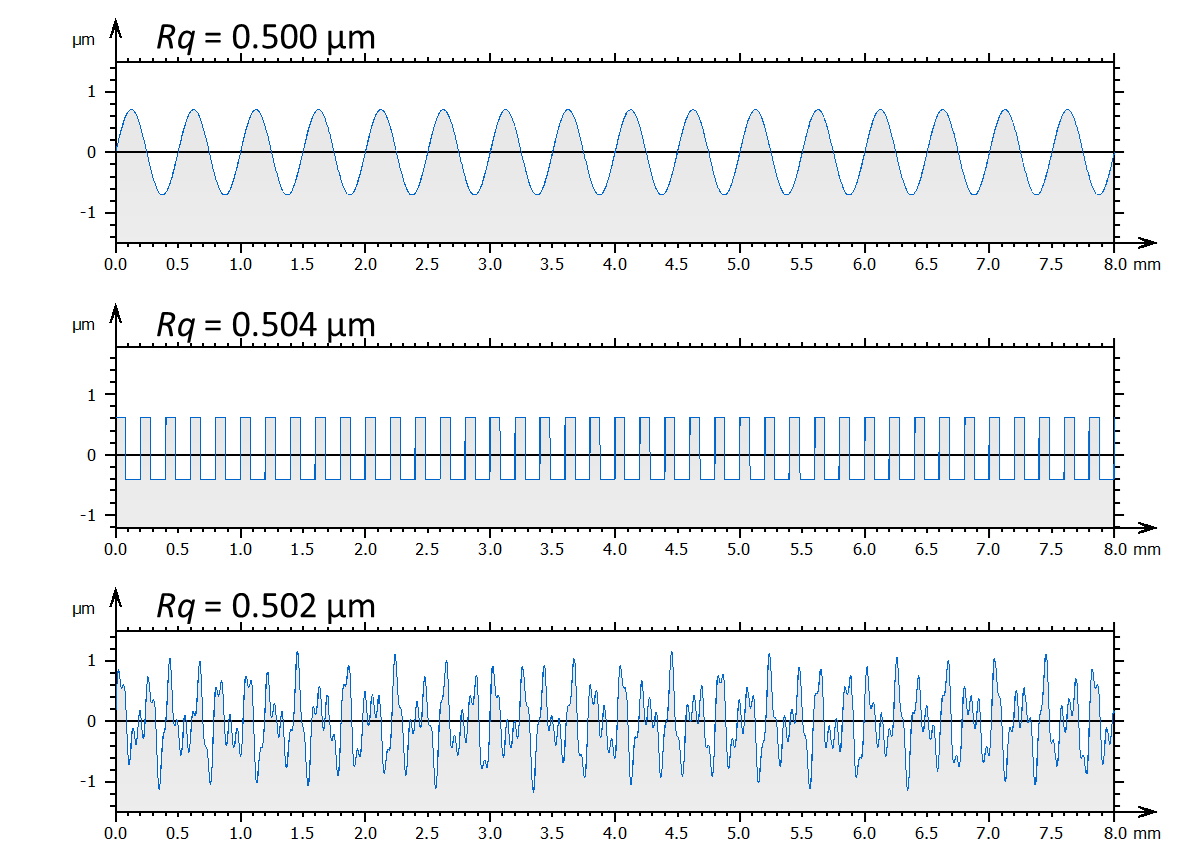
Figure 1. Trois profils avec la même rugosité (Rq, Filtre L, cut-off = 2.5 mm)
mais des longueurs d'ondes moyennes et des formes différentes.



2. Stochastique est-il équivalent à rugueux ?

Evidemment, il y a un lien intuitif et logique entre stochastique et rugueux, et entre déterministe et lisse. Néanmoins, l'axe stochastique-déterministe, parfois nommé en anglais Feature spectrum, n'est pas le même que l'axce rugueux-lisse. On peut même considérer que ce sont deux axes orthogonaux, formant un graphe bidimensionnel dans lequel on peut positionner des matériaux, des procédés de fabrication ou des produits (voir la figure 2).

Ainsi, nous disposons d'un outil nous permettant de catégoriser les surfaces. Dans le quart supérieur gauche de la figure 2, les surfaces rugueux et stochastiques sont obtenues par des procédés de fabrication classiques. Dans le quart inférieur gauche, les surfaces lisses et stochastiques sont obtenues par superfinition ou polissage ou en déposant un revêtement fluide. Dans le quart inférieur droit, les surfaces lisses et déterministes, sont produites par moulage ou lithographie pour créer des micro-structures. Dans le dernier quart, en haut à droite, les surfaces rugueuses et déterministes contiennent des motifs distribués de façon plus naturelles ou organique. De nombreuses autres surfaces ou procédés pourraient être ajoutés à ce graphe.

Un troisième axe pourrait même être imaginé, pour former un graphe tridimensionnel où les surfaces seraient des points dans l'espace, formant un nuage de points, à travers 8 catégories. Ce troisième axe serait l'échele pour souligner le caractère multi-échelle que certaines surfaces peuvent avoir, par exemple, être lisse et stochastique à grande échelle, et rugueux et déterministe à petite échelle.




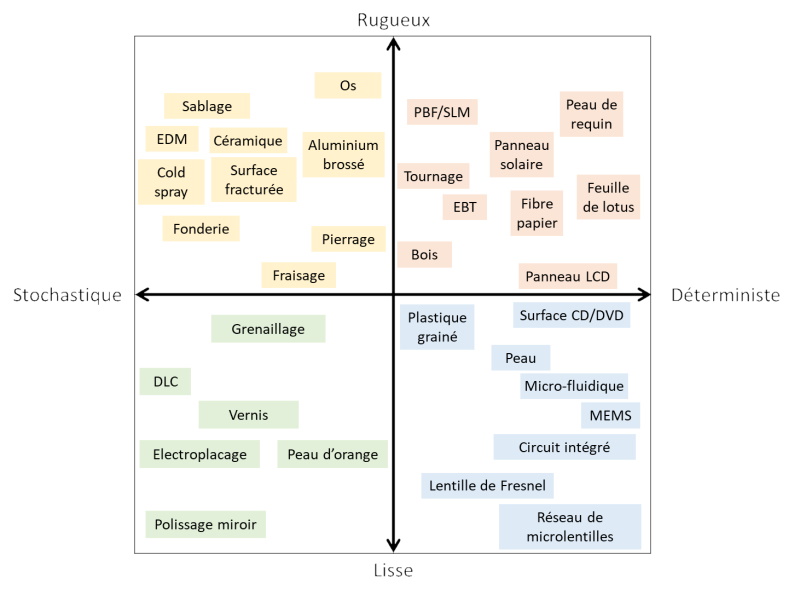
Figure 2. Catégorisation de procédés de fabrication et de matériaux
selon deux axes : stochastique-déterministe et rugueux-lisse.



3. Pourquoi catégoriser

Ces catégories peuvent aider les utilisateurs à choisir l'outil d'analyse adapté à leur surface. Les surfaces stochastiques peuvent être catactérisées à l'aide de paramètres statistiques utilisant tous les points (paramètres de champ). Ces surfaces peuvent habituellement être mesurées en profilométrie de façon fiable car elles sont souvent isotropes. A l'autre bout du spectre, les surfaces déterministes ont des structures ou des motifs qui doivent être caractérisées individuellement, puis les valeurs obtenues peuvent être moyennées sur tous les motifs. Ce genre de surface doit en général être mesuré avec des instruments surfaciques.


4. Lire d'autres ressources


Voir aussi les possibilités d'analyse des surfaces du logiciel MountainsMap® et des modules optionnels.



5. Références bibliographiques