Analyse Fractale Géométrique

1. Qu'est-ce que l'analyse fractale ?

Nous avons tous appris à l'école que les objets géométriques étaient ordonnés selon le nombre de coordonnées nécessaires pour les décrire. Un segment de droite est mono-dimensionnel, un plan est bi-dimensionnel et un cube est tri-dimensionnel. Cependant, dans le monde réel, les lignes peuvent être plus complexes que cela...

Une surface rugueuse est comme une surface montagneuse, à l'échelle microscopique ; sa dimension fractale peut-être vue comme une évaluation de sa complexité. Une surface très lisse et plane aura une dimension fractale proche de 2.0 mais la surface d'une céramique, avec de nombreux pores et cavités aura une dimension fractale plus grande, peut-être plus proche de 3.0 que de 2.0.

Les applications de la théorie de Mandelbrot ont été développées pour l'ingénierie par le professeur Christopher Brown du Worcester Polytechnic Institute (WPI) aux Etats-Unis, qui a introduit le concept d'analyse length-scale et area-scale, ainsi que plusieurs paramètres et méthodes statistiques destinées à établir des corrélations fonctionnelles ou des discriminations.

Ces techniques sont désignées en anglais par l'acronyme SSFA – Scale-Sensitive Fractal Analysis et sont également appelées Geometric Multiscale Analysis.

2. Graphes en fonction de l'échelle

Lorsqu'on utilise l'analyse longueur-échelle (length-scale), un segment de droite de longueur fixe est utilisée comme règle pour mesurer la longueur curviligne du profil (ou d'une ligne d'une surface). La longueur cumulée est divisée par la longueur horizontale pour obtenir une longueur relative. Cette valeur est comprise entre 1.0 et 2.0

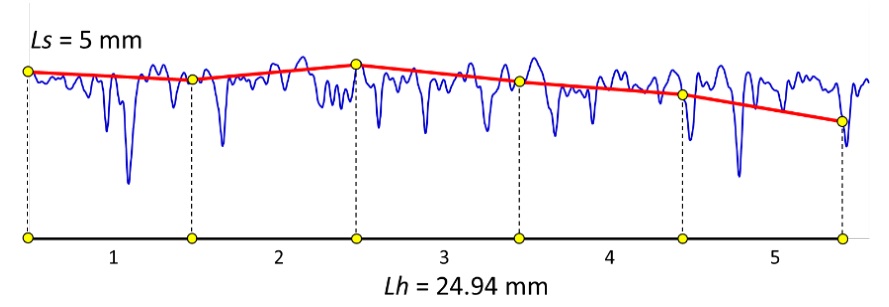
Dans l'exemple ci-dessus, un segment de 5 mm de longueur est utilisé pour mesurer le profil. Un total de 5 segments entiers sont utilisés sur une longueur horizontale de 24,94 mm. La longueur relative est donc de 25,0/24,94 = 1,0024.

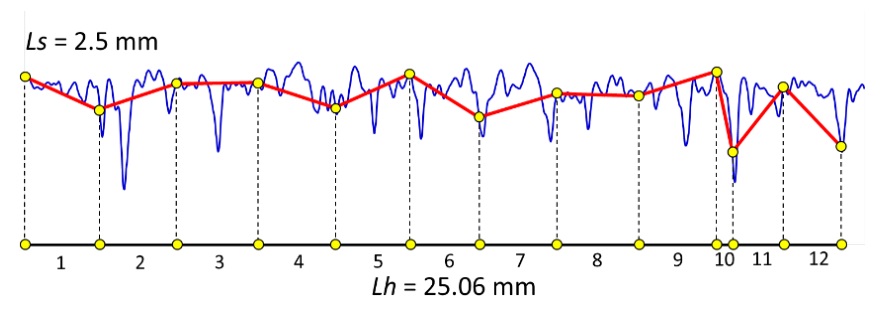
En prenant un segment plus petit de 2,5 mm il est alors possible de mesurer 12 segments entiers sur une longueur horizontale de 25,06 mm, ce qui donne une longueur relative de 1,197. En d'autres mots, plus la règle utilisée pour mesurer le profil est petite, plus la longueur curviligne sera grande et donc la longueur relative sera élevée.

Ce calcul est répété pour un grand nombre de longueurs (d'échelles) depuis le plus grand jusqu'au plus petit, et un graphe est tracé : log(longueur relative) en fonction du log(échelle).

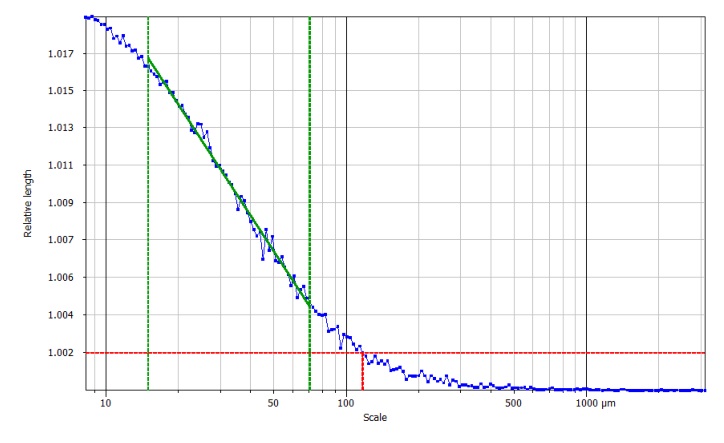
Sur ce graphe, un seuil est utilisé pour trouver le smooth-rough crossover (SRC) qui donne l'échelle à laquelle le régime de la surface passe de lisse à rugueux. Lorsque l'échelle d'analyse est trop grande, la surface est vue comme très lisse et sa dimension fractale est proche de sa dimension euclidienne. Lorsque l'échelle est suffisamment fine pour dévoiler les détails du relief, alors la dimension fractale décrit la complexité de la surface. La partie centrale entre les deux lignes verticales vertes est quasiment linéaire et sa pente permet de calculer la dimension fractale.

3. Une surface peut-elle aussi être analysée avec la même méthode ?

La réponse est oui, puisque la longueur relative peut être calculée sur chaque ligne de la surface, ou sur chaque colonne (rotation de 90°). Une valeur moyenne de chaque ligne est utilisée pour chaque échelle d'analyse, et le même graphe peut être construit.

Une autre méthode, dédiée aux surfaces, la méthode "area-scale" utilise des tuiles triangulaires d'aire fixe pour calculer l'aire curviligne qui est ensuite divisée par l'aire horizontale du support. Un graphe similaire de l'aire relative en fonction de l'échelle peut être construit et les mêmes paramètres évalués.

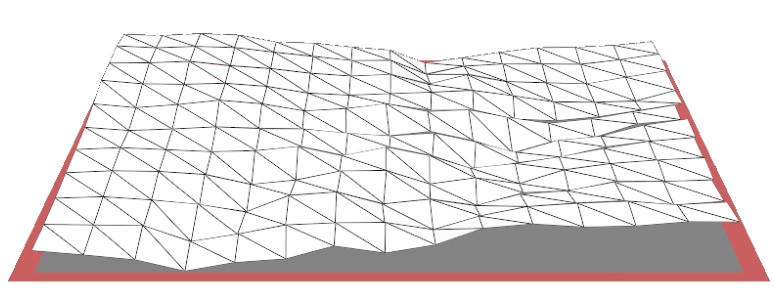
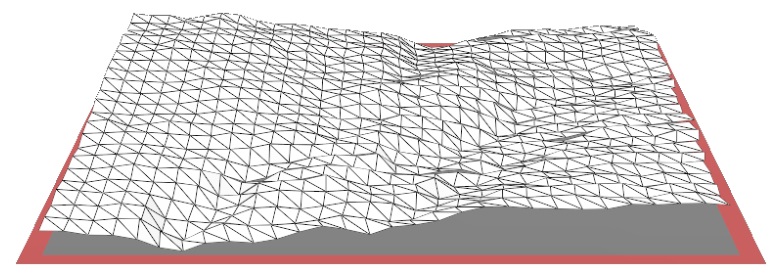
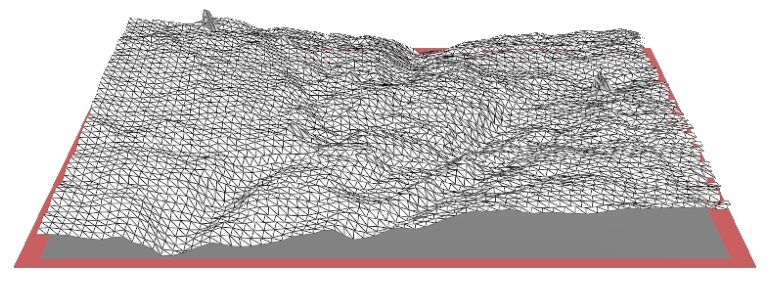
Ci-dessus, trois cas de recouvrement avec des tuiles d'aire différente.

4. Paramètres associés

Ces paramètres sont utilisés dans divers secteurs applicatifs, en métrologie ou en recherche, comme dans l'étude de la force d'adhésion, l'analyse de fractures, les revêtements thermiques, l'usure d'outils, etc.

Smooth-rough crossover / transition lisse/rugueux : ce paramètres est particulièrement utile pour les applications liées à la friction et au contact.

Maximum de la longueur ou de l'aire relative : correspond à la valeur obtenue à l'échelle la plus fine. Sur une surface, cette valeur converge vers le paramètre ISO Sdr (surface développée).

Dimension fractale : calculée sur la partie linéaire du graphe.

Complexité : caractérise de combien la surface est plus complexe qu'un plan euclidien, ou combien un profil est plus complexe qu'une droite euclidienne. Ce concept est plus ou moins équivalent au paramètre ISO Sdq.

Echelle de complexité maximale : échelle pour laquelle la complexité est la plus élevée. Ce paramètre est utilisé dans des études de corrélations avec des attributs fonctionnels.

Coefficient de régression R² : une valeur élevée confirme la pertinence de la valeur de complexité.

Hétérogénéité de la complexité : où une surface est décomposée en blocs (par exemple 5x5) et la dispersion de la valeur de complexité est calculée.

D'autres paramètres spéciaux, initialement développés pour des applications de Dental Microwear Texture Analysis (usure dentaire) par Prof. Rob Scott et Prof. Peter Ungar sont également disponibles.

L'avantage de ces méthodes est que les paramètres sont calculés sur une plage d'échelles où la fonction de la pièce est active. Cette approche multi-échelle est plus pertinente que de calculer un paramètre comme le Sa sur la surface avec un filtre par défaut (qui donne une bande passante pas forcément corrélée avec la fonction).

Voir aussi nos Vidéos de métrologie des surfaces sur l'analyse multi-échelle.

Les paramètres décrits ci-dessus sont définis dans la norme ISO 25178-2:2021, clause 4.7 ainsi que dans l'ASME B46.1:2002.

5. Où trouver ces outils ?

Un module optionnel de MountainsMap^® appelé Scale-Sensitive Fractal Analysis module implémente la plupart des méthodes qui étaient disponibles dans le logiciel Sfrax développé par le professeur Brown. Ce module peut être testé pendant 30 jours et ajouté à une licence existante.