Qu'est-ce que l'analyse spectrale ?

1. Base de traitement du signal

Conduire une analyse spectrale sur un signal signifie examiner son contenu en termes de fréquences (ou de longueurs d'onde). D'après la théorie de Fourier, n'importe quel signal peut être décomposé en une série de signaux élémentaires simples.

Le signal le plus simple est sinusoïdal, qui se définit par sa longueur d'onde, son amplitude et sa phase. La longueur d'onde est la longueur d'une oscillation dans le domaine spatial (donnée en µm, mm ou toute unité de longueur). Si l'onde se propage à une vitesse particulière (notée ν et comptée en m/s) alors on peut définir sa fréquence f = ν/λ, qui est proportionnelle à l'inverse de la longueur d'onde λ.

Dans les états de surface, les signaux sont les profils et les surfaces, donc il est plus pratique de parler en longueur d'onde qu'en fréquence, car les signaux mesurés sont dans le domaine spatial.

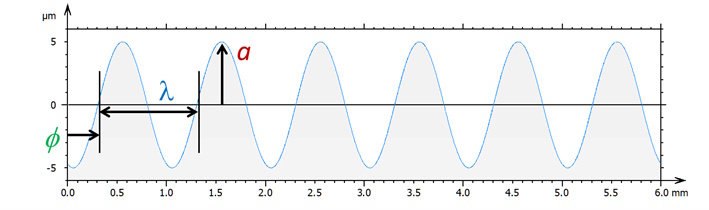
Les trois paramètres qui définissent une onde sinusoïdale : l'amplitude a, la longueur d'onde λ, et la phase Φ.

2. Analyse du contenu spectral d'un signal

Pour passer du domaine spatial au domaine spectral, ou inversement, on utilise une transformée de Fourier, la plupart du temps au travers d'une FFT qui est un algorithme rapide et optimisé. La description spectrale d'un profil ou d'une surface, et leur représentation spectrale, sont deux façons différentes de décrire le même objet. Ce sont des représentations duales.

La representation habituelle d'un spectre est soit un graphe monodimentionnel (1D) qui représente les amplitudes en fonction de l'indice de la fréquence, pour un profil, soit un spectre bidimentionnel (2D) sous forme d'une image qui représente les amplitudes par des couleurs, en fonction des indices X/Y du spectre 2D. En examinant le spectre d'un signal, il est possible d'identifier des oscillations périodiques, qui apparaissent sous forme de pics sur un spectre 1D, ou sous forme de pixels blancs sur un spectre 2D.

Les pics spectraux peuvent représenter des structures réelles sur la surface, telles que les motifs périodiques d'un étalon triangulaire, ou peuvent être également des oscillations parasites dues à des vibrations ou la réjection de la fréquence électrique de l'alimentation (à 50 ou 60 Hz).

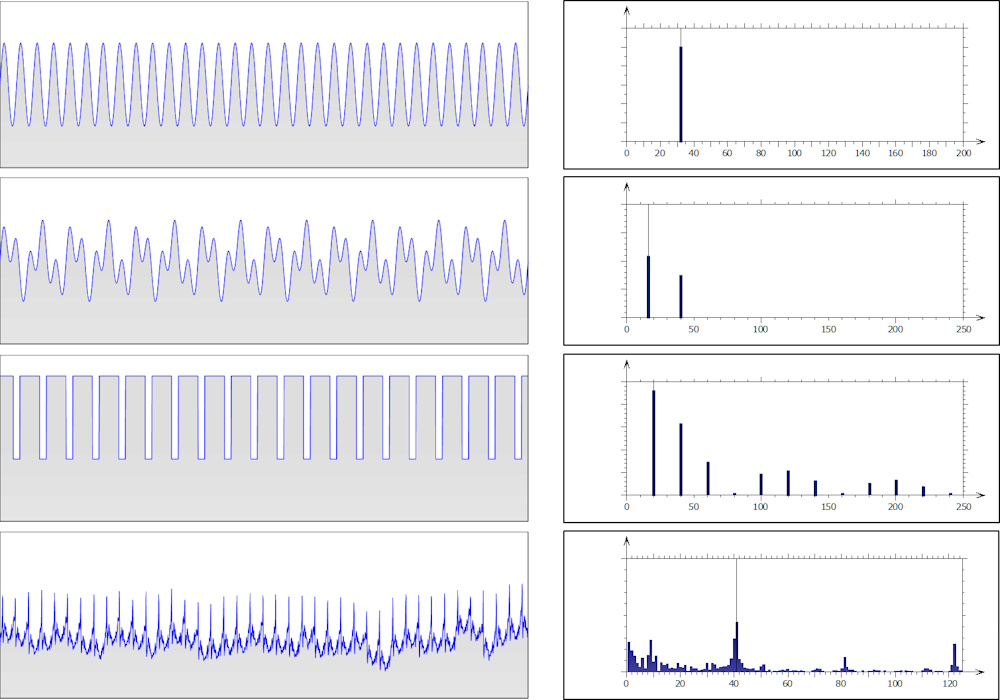
La figure ci-contre, montre plusieurs profils et leur spectre respectif. Le spectre d'une onde parfaitement sinusoïdale est représenté, par définition, sous la forme d'un pic unique, puisque se décomposition spectrale n'a qu'un seul terme.

Un signal composé de deux sinusoïdes à des fréquences et amplitudes différentes aura un spectre composé de deux pics spectraux.

Un signal un peu plus complexe, tel qu'un signal carré périodique avec un rapport cyclique non symétrique donnera un spectre un peu plus étoffé constitué de la fréquence fondamentale de la période principale, plus les harmoniques complémentaires qui définissent la forme carrée et qui sont des multiples de la fréquence fondamentale.

Enfin, dans le cas d'un profil réel périodique, qui contient des irrégularités, on obtient un spectre contenu la fréquence fondamentale et ses harmoniques, mais également un continuum de raies spectrales autour, qui représentent les irrégularités du profil.

3. Filtrage

Le but d'un filtrage est d'atténuer une partie du spectre pour transmettre l'autre partie. Par exemple, en atténuant les grandes longueurs d'onde d'un profil primaire, au-dessus d'une valeur de cut-off (λc ou Nic), on obtient le profil de rugosité. C'est donc un Filtre L (ou un filtre passe-haut). Un filtre de micro-rugosité, qui retire les longueurs d'onde les plus courtes, en-dessous de λs (ou de Nis) est un Filtre S.

Les différents types de filtres (gaussien, spline, gaussien robuste) ont des courbes de réponse différentes en fréquence mais sont tous basés sur le même principe d'attenuation d'une partie du spectre. Ces filtres sont décrits dans la série de normes ISO 16610.

4. Outils logiciels d'analyse spectrale

Dans le logiciel Mountains®, plusieurs opérateurs et études permettent d'analyser le contenu spectral ou de le modifier. L'opérateur Filtrer le spectre permet de modifier de façon interactive le contenu spectral d'un profil ou d'une surface. L'opérateur Seuiller le spectre fournit un moyen facile de supprimer le bruit ou des fréquences parasites.

L'étude Spectre fréquentiel affiche un curseur sur le spectre, permettant de vérifier la longueur d'onde, l'amplitude et la phase d'un pic spectral particulier. L'étude Densité spectrale de puissance moyennée fournit un rendu plus détaillé des grandes longueurs d'onde et dispose d'un mode pour évaluer la DSP pour des applications optiques.

D'autres fonctions d'analyse spectrale sont également disponibles dans le logiciel. Voir les pages sur le logiciel Mountains® et ses modules optionnels.