Die ersten Hersteller von Messinstrumenten für flächenhafte Oberflächenbeschaffenheit haben zunächst Charakterisierungsmethoden vorgeschlagen, die hauptsächlich auf einer einfachen Extrapolation von 2D-Methoden beruhten. In Abwesenheit offizieller Dokumentation dachten sich die Hersteller mehr oder weniger gelungene Lösungen aus, wobei die Oberflächenparameter manchmal als das einfache Mittel der Profilparameter berechnet wurden, die für jede Linie auf der Oberfläche ausgewertet wurden, oder für radiale Profile, die aus einem Kreis mit Ursprung in der Mitte des Bildes extrahiert wurden.
Die Benennungsregeln für die Parameter wurden auch aus den 2D-Parametern abgeleitet (sRa, sWa ...) und mit Hilfe von proprietären Algorithmen berechnet; dies führte zu unterschiedlichen Werten auf verschiedenen Instrumenten. Trotzdem wurden bewährte Praktiken später verbreitet, vor allem dank der Publikationen von Pr. Stout und seiner Mitarbeiter in Birmingham[STOUT 1993], und mit der Einführung der von Digital Surf entwickelten DigiSurface-Software auf Macintosh im Jahr 1993, die später an Taylor Hobsons Form Talysurf unter dem Namen Talymap angepasst wurde. Später haben die Einführung von MountainsMap im Jahre 1996 und die Veröffentlichung des SurfStand-Reports [BLUNT 2003] dazu beigetragen, Standard-Methoden zur Berechnung flächenhafter Oberflächenbeschaffenheits-Parameter zu verbreiten. MountainsMap® Version 5.0 war das erste kommerzielle Paket, das im Jahr 2007 das komplette Set der im Entwurf ISO 25178 definierten Flächenparameter anbietet.

Details zu Flächenparametern
finden Sie in [BLATEYRON 2013a] (Kapitel 2 von [LEACH 2013]).
Benennungsregeln für 3D-Parameter
In der Norm ISO 25178 beginnen alle flächenhaften Parameter mit dem Großbuchstaben S oder dem Großbuchstaben V. Im Gegensatz zu Benennungsregeln, die mit Profilparametern verwendet werden, spiegeln Präfixe der flächenhaften Parameter nicht die Art der Oberfläche wider, die zwischen Rauheit und Welligkeit unterscheidet. Für Profile haben wir Pa, Ra und Wa; Für Flächen haben wir nur Sa, der daher ein Parameter der Rauheit oder Welligkeit sein kann oder auf der Primärfläche berechnet sein kann, abhängig von der Vorfilterung, die durchgeführt wird, bevor der Parameter berechnet wird. Diese Entscheidung basiert auf der Vielzahl von Verarbeitungs- und Filtermethoden, die Metrologen zur Informationsgewinnung aus einer Oberfläche zur Verfügung stehen [ISO 16610]. Diese Verarbeitungsmethoden trennen nicht notwendigerweise die Oberflächenbeschaffenheit in die zwei Komponenten Rauheit und Welligkeit, sondern verändern in gewissen Fällen die Oberfläche in einer subtileren Weise.
Amplituden-Parameter
Die meisten der in ISO 4287 definierten Profilparameter haben eine mathematische Gleichung, die leicht auf Oberflächen übertragen werden kann. Sq ist beispielsweise einfach eine Erweiterung zur Ebene der Gleichung für Rq, die für eine Gerade definiert ist:
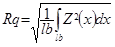
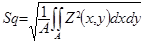
Sa, Sq, Ssk, Sku, Sp, Sv, etc. können daher in gleicher Weise genauso einfach definiert werden.
Parametergleichungen verwenden Integrale anstelle von Summen, da die Definitionen für den kontinuierlichen Fall gelten. Natürlich verwenden praktische Implementierungen diskrete Daten und verschiedene Annäherungen an die Integration. Es wird keine empfohlene Methode angegeben, aber jeder Algorithmus zeichnet sich durch mehr oder weniger Unsicherheit aus.
Neben den oben genannten Parametern, die leicht extrapoliert werden können, stellen bestimmte Parameter Probleme dar. Rz ist in ISO 4287 als maximale Höhe auf einer Einzelmessstrecke definiert und wird über die in der Messstrecke enthaltene Anzahl an Einzelmessstrecken gemittelt. Im Allgemeinen ist Rz kleiner als Rt. Dieser Parameter hatte schon zahlreiche Definitionen, die zuerst in ISO 4287 (1984) als Zehn-Punkte-Höhe definiert waren und dann 1997 geändert wurden, und er ist vor allem wegen seiner Ähnlichkeiten mit den Ry- und Rmax-Parametern verwirrend geblieben.
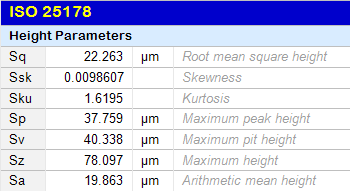
Beachten Sie, dass Sz, so wie er in ISO 25178 definiert ist, einfach die maximale Höhe vom höchsten Punkt zum tiefsten Tal ist, was der früheren Definition von St entspricht. Deswegen ist St nicht mehr in der Norm aufgeführt! Das Fehlen dieses bekannten Parameters kann einige Benutzer verwirren!
Räumliche Parameter
Eine Oberfläche wird isotrop genannt, wenn sie unabhängig von der Messrichtung identische Eigenschaften aufweist. Dies ist zum Beispiel für Flächen mit einer zufälligen Oberflächenstruktur der Fall, die keine hervorstehende Textur aufweisen. Diese Art von Oberfläche ist leider ziemlich selten, und die meisten industriell hergestellten Oberflächen haben eine orientierte Oberfläche (gedrehte, geschliffene oder gebürstete Flächen) oder eine periodische Struktur (EBT-Oberflächen (Electron-Beam-Texturing), genarbte Kunststoffe). In diesem Fall sagt man, dass die Oberfläche anisotrop ist.
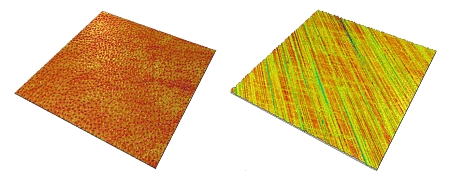
Isotrope Oberfläche (links) - anisotrope Oberfläche (rechts)
Die Isotropie einer Oberfläche kann durch Werkzeuge beeinflusst und quantifiziert werden, die auf Fourier-Transformation und Autokorrelation beruhen.
Autokorrelation ist eine Funktion, die durch folgende Gleichung beschrieben wird:
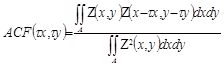
Diese Funktion ermöglicht es, ein Bild zu erzeugen, auf dem charakteristische Größen gemessen werden können.
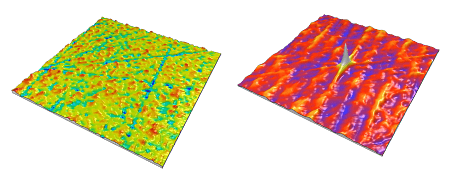
Oberfläche (links) - Autokorrelation (rechts)
Das Autokorrelationsbild enthält immer eine zentrale Spitze mit einer normalisierten Amplitude von 1,0. In einigen Fällen enthält das Bild sekundäre Spitzen, die eine gewisse Korrelation zwischen Teilen der Oberfläche und der Oberfläche selbst aufzeigen. Dies ist bei Flächen mit periodischen oder pseudo-periodischen Motiven der Fall. In der Tat ist die Form der zentralen Spitze ein Indikator für die Isotropie der Oberfläche.
Um die Form der zentralen Spitze zu charakterisieren, wird ein Schwellenwert s von 0,2 verwendet; danach wird die zentrale Zone des Bildes quantifiziert, die dem verbleibenden Teil der Spitze entspricht.
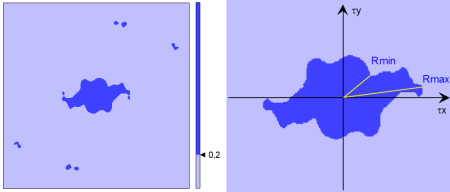
Auf diese Weise ist es möglich, einen Parameter zu erhalten, der ein Indikator für die Oberflächenisotropie ist:
Str, Textur-Aspekt-Verhältnis
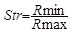
Die minimalen und maximalen Radien werden auf dem Bild des zentralen Lappens gesucht (der mithilfe des Schwellenwert-Setzens auf der zentralen Autokorrelationsspitze erhalten wurde). Wenn die Oberfläche in jeder Richtung die gleichen Eigenschaften aufweist, dann ist der zentrale Lappen etwa kreisförmig und die minimalen und maximalen Radien sind ungefähr gleich. Wenn die Oberfläche eine starke hervorstechende Orientierung aufweist, dann ist der zentrale Lappen sehr langgezogen, und der maximale Radius viel größer als der minimale Radius.
wobei Rmin und Rmax die minimalen und maximalen Radien sind, die in Bezug auf den Umfang des zentralen Lappens berechnet wurden. Die Radien werden aus den Koordinaten des Punktes (tx, ty) auf dem Umfang berechnet. Beachten Sie, dass der Schwellenwert von 0,2 ein Standardwert ist, dass es aber für bestimmte Anwendungen ratsam sein kann, einen höheren oder niedrigeren Wert zu wählen, insbesondere um sicherzustellen, dass der zentrale Lappen gut definiert ist und nicht die Kanten des Bildes berührt. Der Str-Parameter ergibt Werte zwischen 0 und 1 und hat keine Einheit. Er kann auch als Prozentsatz zwischen 0 % und 100 % ausgedrückt werden. Eine isotrope Oberfläche hat einen Str nahe 1 (100 %), während eine stark anisotrope Oberfläche einen Str-Wert nahe 0 hat.
Der Wert Rmin liefert ebenfalls einen nützlichen Hinweis auf den spektralen Inhalt der Oberfläche. Eine Oberfläche, die im wesentlichen aus Spektralkomponenten mit langen Wellenlängen besteht, ergibt einen hohen Rmin und umgekehrt. Daher ist der Parameter Sal wie folgt definiert:
Sal, Länge des schnellsten Abklingens der Autokorrelation Sal = Rmin
Dieser Parameter wird in μm ausgedrückt.
Ein weiteres nützliches Werkzeug ist das Polarspektrum. Wenn es in Polarkoordinaten integriert ist, ermöglicht das Fourier-Spektrum es, die privilegierte Richtung der Oberflächenstrukturen zu bestimmen. Das Polarspektrum berücksichtigt das Leistungsspektrum der Oberfläche in jeder Richtung. Der Winkel mit dem größten Leistungsspektrum entspricht der privilegierten Texturrichtung.
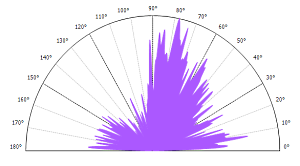
Die Darstellung des Polarspektrums zeigt deutlich die privilegierten Richtungen. Der Winkel, der dem Maximum des Polarspektrums entspricht, ermöglicht es, den Std-Parameter zu definieren:
Std, Texturrichtung
Dieser Winkel wird gegen den Uhrzeigersinn in Grad ausgedrückt.
Die grundlegenden Amplitudenparameter sind in allen MountainsMap-Produkten enthalten. Räumliche, hybride und funktionale Parameter sind Teil des optionalen Moduls 3D Advanced Surface Texture und sind in MountainsMap Premium enthalten.
Nächste Seite Flächenhafte (Flächen-)Funktions-Parameter