


History of surface texture metrology until the latest ISO 25178 standard on areal surface texture.
Introduction to ISO 25178, the standard on areal surface texture that describes parameters, instruments, etc.
The recent revision of ISO 25178-2 in December 2021 fixes several errors and introduces new parameters.
Areal field parameters from ISO 25178-2, with amplitude parameters (Sa, Sq, etc.) and spatial and hybrid parameters (Sdr, Sal, etc.).
Areal functional parameters on bearing ratio, Sk parameters, functional indices and volume parameters, largely used in the automotive industry.
Areal feature parameters calculated by segmentation, that allows the characterization of specific structures.

This video introduces the reasons why surface texture is specified and verified on engineered products, and gives the basic concepts you should know before using surface texture analysis. Duration: 10 min 58
View other surface metrology videos.
Panorama of parameters defined in various standards for the evaluation of roughness and waviness profiles.
Introduction to the new standard that will modernize profilometry and that should replace all previous profile standards.
Introduction to the classical roughness parameters, in particular Ra, Rz or RSm, and their waviness and primary equivalent.
This standard is used in the automotive industry to caracterize profile motifs, close to functional requirements.
This standard specializes on functional stratified surfaces made by a multipass manufacturing process.
And also:

This video explains the modifications introduced to surface texture parameters in the new ISO 21920 standard, compared to former standards ISO 4287, ISO 4288, ISO 1302, ISO 13565, etc. Duration: 13 min 27
View other surface metrology videos.
Methods of leveling and form removal required to create the primary profile or the SF surface.
Explore filtration operators and several filters defined in ISO 16610 as well as other innovative applications.
A powerful multi-scale geometrical analysis to explore profile and surface behaviors and their relation to function.
Learn about the next revolution on surface analysis, suitable for additive manufactured surfaces.
And also:

This video introduces the bases of filtration in surface texture and explains how filters act on the spectral content of profiles and surfaces. Duration: 19 min 57
View other surface metrology videos.
How to write surface texture specifications on a technical drawing, according to ISO 1302.
Series of on-line video courses about surface texture metrology. The videos are free to use. They are available in English or in French with English sub-titles.
This section provides a list of important ISO and national standards in the field of surface texture.
Comprehensive bibliography of scientific papers and metrology books that are useful for surface texture analysis.
And also:
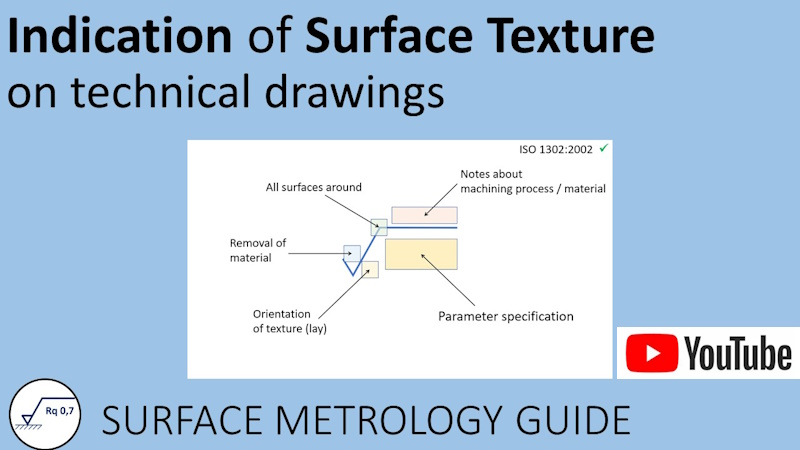
This video introduces the graphical language used to indicate surface texture specifications on technical drawings, according to ISO 1302. Changes introduced by the new ISO 21920-1 are also discussed.
Duration: 15 min 04
View other surface metrology videos.